Preface

　このシリーズでは、Diffusionモデルについて学習する時にノート代わりに記事を書いていく。これはその第二弾で以下の第一弾の続き。手始めにめちゃ分かりやすいと巷で話題の（そして実際分かりやすかった）以下のDiffusionモデルの解説論文を少しずつ翻訳していき、脳に焼き付けていく。後々より詳しい解説とか、自分でJAXで実装とかができたらいいなと思っている。

izmyon.hatenablog.com

Preface
Understanding Diffusion Models: A Unified Perspective

arxiv.org

Calvin Luo: Understanding Diffusion Models: A Unified Perspective, arXiv: 2208:11970, doi: 10.48550/ARXIV.2208.11970

©Calvin Luo, Originally posted in arXiv(https://arxiv.org/abs/2208.11970), 25 Aug 2022

License: Creative Commons Attribution 4.0 International (CC-BY)

以下は、原文の一部を翻訳したもので、以下の図はそこから引用したものです。

The following is the translation of part of the original content and the figures below are retrieved from it.

Understanding Diffusion Models: A Unified Perspective

Variational Diffusion Model

Learning Diffusion Noise Parameters

ここで、VDMのノイズパラメータをどのように同時学習させるかを検討しよう。一つの方法として、パラメータ $\eta$ を持つニューラルネットワーク $\hat{\alpha}_{\eta} (t)$ を用いて $\alpha_t$ をモデル化することが考えられる。しかし、これは $\hat{\alpha}_t$ を計算するたびに推論を複数回行わなければならず、非効率的である。キャッシュはこの計算コストを軽減することができるが、我々は拡散ノイズのパラメータを学習する別の方法を導き出すことができる。式(85)の分散方程式を式(99)のタイムステップごとの目的関数に代入することで、削減することができる。

式(70)から、 $q(x_t | x_0)$ は $\mathcal{N} \left( x_t; \sqrt{\alpha_t} x_0, (1- \alpha_t ) \boldsymbol{\rm{I}} \right)$ 形式のガウスであることを想起してほしい。そして、信号対雑音比（SNR）の定義である $\rm{SNR}＝\frac{ μ^ 2 }{ \sigma^ 2}$ に従って、各タイムステップにおけるSNRを以下のように書ける。

$\rm{SNR} (t) = \frac{\bar{\alpha}_t}{1- \bar{\alpha}_t} \tag{109}$

そうすると、私たちが導き出した式(108)（および式(99)）は、次のように簡略化できる。

$\frac{1}{2 \sigma_q^2 (t) } \frac{ \bar{\alpha}_{t-1} \left(1- \alpha_t \right)^2 }{ \left( 1 - \bar{\alpha}_t \right)^2 } \left[ \left|| \hat{x}_{\theta} (x_t, t) - x_0 \right||_2^2 \right] = \frac{1}{2} \left( \rm{SNR} (t-1) - \rm{SNR} (t) \right) \left[ \left|| \hat{x}_{\theta} (x_t, t) - x_0 \right||_2^2 \right] \tag{110}$

その名が示す通り、SNRは、元の信号と含有されるノイズ量の比率を表している。SNRが高いほど元の信号が多く、SNR が低いほどノイズが多いことを意味する。拡散モデルでは、SNRは時間と共に単調に減少させる必要がある。これは、摂動入力 $x_t$ は時間とともにノイズが多くなり、 $t=T$ で標準ガウスと同じになるという概念を正式に示すものである。

式(110)の目的関数を単純化すると、ニューラルネットワークを用いて各タイムステップのSNRを直接パラメータ化し、拡散モデルと同時に学習させることができる。SNRは時間と共に単調に減少しなければならないので、次のように表すことができる。

$\rm{SNR} (t) = exp(-\omega_{\eta} (t) ) \tag{111}$

ここで $\omega_{\eta} (t)$ はパラメータ $\eta$ を持つ単調増加ニューラルネットワークとしてモデル化されている。 $\omega_{\eta} (t)$ を判定にすると単調減少する関数になるが、指数関数では結果として生じる項が正になるように強制される。式(100)の目的関数は $\eta$ についても最適化しなければならないことに注意してほしい。式(111)のSNRのパラメータ化と式(109)のSNRの定義を組み合わせることにより、 $\alpha_t$ の値と $1- \bar{α}_t$ の値についてエレガントな形を明示的に導き出すことも可能である。

$\begin{align} \frac { \bar{\alpha_t} }{1- \bar{\alpha_t}} &= \rm{exp} \left( - \omega_{\eta} (t) \right) \tag{112} \\ \therefore \bar{\alpha_t} &= \rm{sigmoid} \left( - \omega_{\eta} (t) \right) \tag{113} \\ \therefore 1- \bar{\alpha_t} &= \rm{sigmoid} \left( \omega_{\eta} (t) \right) \tag{114} \end{align}$

これらの項は様々な計算に必要であり、例えば最適化の際には、式(69)で導かれるように、再パラメータ化トリックを用いて、入力 $x_0$ から任意のノイズの多い $x_t$ を作成するために使用される。

Three Equivalent Interpretations

先に証明したように、変分拡散モデルの学習は、単に任意のノイズ処理された画像 $x_t$ とその時刻 $t$ から、元の自然画像 $x_0$ を予測するニューラルネットワークを学習するだけで可能である。しかし、 $x_0$ は他に2つの等価なパラメタリゼーションを持つので、VDMはさらに2つの解釈をすることができる。

まず、再パラメータ化のトリックを用いる。 $q_(x_t|x_0)$ の形の導出において、式(69)を並べ替えて、次のように示すことができる。

$x_0 = \frac{x_t - \sqrt{1- \bar{\alpha}_t}\epsilon}{\sqrt{ \bar{\alpha}_t}} \tag{115}$

これを先に導いた真のノイズ除去遷移における平均 $μ_q(x_t,x_0)$ に代入すると、次のように再導出できる。

したがって、近似的なノイズ除去遷移の平均 $μ_{\theta} (x_t,t)$ を次のように設定することができる。

$\mu_{\theta} (x_t, t) = \frac{1}{ \sqrt{\alpha_t} } x_t - \frac{ 1-\alpha_t }{ \sqrt{1- \bar{\alpha}_t} \sqrt{\alpha_t} } \hat{\epsilon}_{\theta} (x_t, t) \tag{125}$

そうすると、対応する最適化問題は次のようになる。

ここで、 $\hat{\epsilon}_{\theta} (x_t, t)$ は $x_0$ から $x_t$ を決定するソース雑音 $\boldsymbol{\epsilon}_0 \sim \mathcal{N} \left( \boldsymbol{ \epsilon ; 0, \rm{I}} \right)$ を予測するように学習するニューラルネットワークである。したがって、元画像 $x_0$ を予測してVDMを学習することは、ノイズを予測するように学習することと同等であることを示したが、経験的には、ノイズを予測した方が性能が良いという研究もある[5, 7]。

変分拡散モデルの三つ目の共通解釈を導出するため、我々はTweedieの公式[8]に訴える。Tweedieの公式は、指数関数型分布の真の平均は、その分布から得られた標本が与えられたとき、標本の最尤推定値（別名：経験平均）に推定値のスコアを含む何らかの補正項を加えたもので推定できることを述べている。観測された標本が1つだけの場合、経験平均は標本そのものである。もし、観測された標本がすべて基本分布の一方の端にある場合、負のスコアが大きくなり、標本のナイーブな最尤推定値を真の平均に向かって修正する。これは、標本の偏りを軽減するためによく使われる。

数学的には、ガウス変数 $z \sim \mathcal{N} \left( z; \mu_ z, {\sum}_ z \right)$ に対して、Tweedieの公式は次のようになる。

$\mathbb{E} \left[ \mu_z | z \right] = z + {\sum}_z \nabla_z \log p (z)$

この場合、その標本が与えられたときの $x_t$ の真の事後平均を予測するために適用する。式(70)から、次のことがわかる。

$q (x_t | x_0) = N \left( x_t; \sqrt{\bar{\alpha}_t} x_0, (1- \bar{\alpha}_t) \boldsymbol{\rm{I}} \right)$

すると、Tweedieの式により、次のようになる。

$\mathbb{E} \left[ \mu_z | x_t \right] = x_t + (1- \bar{\alpha}_t) \nabla_{x_t} \log p( x_t ) \tag{131}$

ここで、表記を簡単にするために、 $\nabla_{x_t} \log p (x_t)$ を $\nabla \log p(x_t)$ と書く。Tweedieの式によれば、 $x_t$ が生成される真の平均の最良推定値 $\mu_{x_t}= \sqrt{\alpha_t} x_0$ は、次式で定義される。

$\begin{align} \sqrt{\bar{\alpha}_t} x_0 = x_t + \left( 1- \bar{\alpha}_t \right) \nabla \log p(x_t) \tag{132} \\ \therefore x_0 = \frac{ x_t + \left( 1- \bar{\alpha}_t \right) \nabla \log p(x_t)}{\sqrt{\bar{\alpha}_t}} \tag{133} \end{align}$

次に、式(133)を、ground-truthのノイズ除去遷移の平均 $μ_q (x_t, x_0)$ にもう一度代入すると、新しい形が得られる。

したがって、近似的なノイズ除去遷移の平均 $\mu_{\theta} (x_t, t)$ を次のように設定することもできる。

$\mu_{\theta} (x_t, t) = \frac{1}{ \sqrt{\alpha_t} } x_t + \frac{ 1- \alpha_t }{ \sqrt{\alpha_t} } s_{\theta} (x_t, t) \tag{143}$

すると、対応する最適化問題は次のようになる。

ここで、 $s_{\theta} (x_t, t)$ は任意のノイズレベル $t$ に対して、データ空間における $x_t$ の勾配であるスコア関数 $\nabla_{x_t} \log p(x_t)$ を予測するように学習するニューラルネットである。

鋭い読者なら、スコア関数 $\nabla \log p(x_t)$ がソース雑音 $\epsilon_0$ と非常によく似た形をしていることに気づくだろう。このことは、Tweedieの公式(式(133))とパラメータ化のトリック(式(115))を組み合わせることで、明示的に示すことができる。

$\begin{align} x_0 = \frac{x_t + (1- \bar{\alpha}_t) \nabla \log p(x_t) }{ \sqrt{ \bar{\alpha}_t } } &= \frac{x_t - \sqrt{1- \bar{\alpha}_t} \epsilon_0}{ \sqrt{ \bar{\alpha}_t } } \tag{149} \\ \therefore (1- \bar{\alpha}_t) \nabla \log p(x_t) &= - \sqrt{1- \bar{\alpha}_t} \epsilon_0 \tag{150} \\ \nabla \log p(x_t) &= - \frac{1}{\sqrt{1- \bar{\alpha}_t}} \epsilon_0 \tag{151} \end{align}$

その結果、2つの項は時間と共に変化する定数だけずれていることがわかる！スコア関数は、対数確率を最大化するようにデータ空間をどのように移動すればよいかを測るのである。直感的には、ノイズは自然な画像に付加され、画像を劣化させるので、その反対方向に移動することが画像を「ノイズ除去」し、その後の対数確率を増加させるための最善の更新となる。我々の数学的証明はこの直感を正当化するもので、スコア関数をモデル化する学習は（スケーリングファクターまで）ソースノイズの負のモデルを作ることと等価であることを明示的に示している。

したがって我々は、VDMを最適化するための3つの等価な目的を導き出した。それは、元の画像 $x_0$ 、ソース雑音 $\epsilon_0$ 、または任意のノイズレベル $\nabla \log p(x_t)$ における画像のスコアを予測するニューラルネットワークを学習することであった。VDMは、確率的に時間ステップ $t$ をサンプリングし、予測値とground-truth目標値との差を最小化することで、スケーラブルに学習することができる。

Score-based Generative Models

我々は、単にスコア関数 $\nabla \log p(x_t)$ を予測するニューラルネットワーク $s_{\theta} (x_t, t)$ を最適化することによって、変分拡散モデルが学習できることを示した。しかし、この導出ではスコア項はTweedieの公式を応用したものであり、スコア関数とは何か、なぜそれがモデル化する価値があるのかについて、必ずしも大きな直感や洞察を与えてくれるものではない。幸いなことに、この直感を得るために、別のクラスの生成モデルであるスコアベース生成モデル[9, 10, 11] に注目することができる。その結果、我々が以前に導出したVDMの定式化は、同等のスコアベース生成モデリングの定式化を持つことを示すことができ、この2つの解釈を自在に切り替えることができるようになったのである。

図6：ランジュバン動力学で生成された三つのランダムなサンプリング軌道の視覚化。すべてのサンプルは混合ガウシアンに対して、同じ初期化点から出発している。左図はこれらのサンプリング軌道を三次元コンター上にプロットしたものであり、右図はサンプリング軌道をground-truthのスコア関数に対してプロットしたものである。同じ初期化点から、異なるモードのサンプルを生成できるのは、ランジュバン動力学のサンプリング手順に含まれる確率的ノイズ項によるものである。これがなければ、固定点からのサンプリングは常に各試行ごとに同じモードへのスコアを決定論的に追従することになる。

なぜスコア関数を最適化することが意味を持つのかを理解するために、回り道をしてエネルギーベースのモデル[12, 13]を再検討してみることにする。任意に柔軟な確率分布は次のような形で書くことができる。

$p_{\theta} (x) = \frac{1}{Z_{\theta}} e^{- f_{\theta} (x)} \tag{152}$

ここで、 $f_{\theta} (x)$ はエネルギー関数と呼ばれる任意に柔軟でパラメータ化可能な関数で、しばしばニューラルネットワークによってモデル化され、 $Z_{\theta}$ は $\int p_{\theta} (x) dx = 1$ を保証するための正規化定数である。このような分布を学習する一つの方法は最尤法であるが、これは正規化定数 $Z_{\theta} = \int e^{ - f_{\theta} (x)}$ を扱いやすく計算する必要があり、これは複雑な $f_{\theta} (x)$ を持つ関数では不可能かもしれない。

正規化定数を計算またはモデル化するのを避ける一つの方法は、ニューラルネットワーク $s_{\theta} (x)$ を、分布 $p(x)$ のスコア関数 $\nabla \log p(x)$ を学習するために代わりに使用することである。これは、式(152)の両辺のlogの導関数を取ると、得られるという観察によって動機づけられている。

$\begin{align} \nabla_x \log p_{\theta} (x) &= \nabla_x \log \left( \frac{1}{Z_{\theta}} e^{- f_{\theta} (x)} \right) \tag{153} \\ &= \nabla_x \log \frac{1}{Z_{\theta}} + \nabla_x \log e^{- f_{\theta} (x)} \tag{154} \\ &= - \nabla_x f_{\theta} (x) \tag{155} \\ &\approx s_{\theta} (x) \tag{156} \end{align}$

これは、正規化定数を必要とせず、自由にニューラルネットワークとして表現することができる。また、スコアモデルは、Fisherダイバージェンスをground-truthのスコア関数と比較して最小化することにより最適化することができる。

$\mathbb{E}_{p(x)} \left[ \left|| s_{\theta} (x) - \nabla \log p(x) \right||^2_2 \right] \tag{157}$

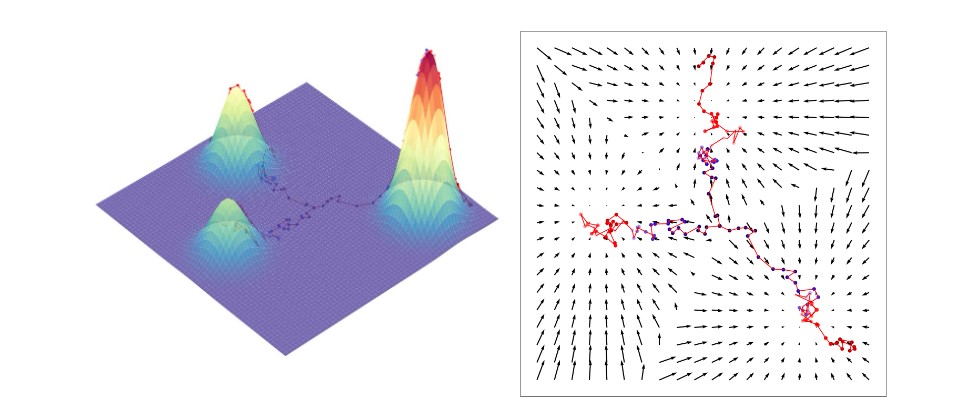
スコア関数は何を表しているだろうか？すべての $x$ について、 $x$ に関する対数尤度の勾配をとることで、尤度をさらに高めるためにデータ空間のどの方向に移動すべきかを本質的に記述する。直感的には、スコア関数はデータ $x$ が存在する空間全体に対してベクトル場を定義しており、そのベクトルはモードを指示している。視覚的には、図6の右図のようになる。そして、真のデータ分布のスコア関数を学習することで、同じ空間内の任意の点から出発し、モードに達するまでスコアを繰り返し追いながらサンプルを生成することができる。このサンプリング方法はランジュバン動力学として知られており、数学的には次のように記述される。

$x_{i+1} \leftarrow x_i + c \nabla \log p(x_i) + \sqrt{2c} \epsilon, \quad i=0, 1, \ldots , K \tag{158}$

ここで、 $x_0$ は事前分布（一様分布など）からランダムにサンプリングされ、 $\epsilon \sim \mathcal{N} (\boldsymbol{\epsilon ;0,I})$ は生成されたサンプルが常にあるモードに収束せず、その近傍を推移して多様性を確保するための追加的なノイズ項である。さらに、学習されたスコア関数は決定論的であるため、ノイズ項を導入したサンプリングは生成過程に確率性を与え、決定論的な軌道を回避することができる。これは、複数のモードの間にある位置からサンプリングを初期化する場合に特に有効である。図6に、ランジュバン動力学のサンプリングとノイズ項の効果を視覚的に表現したものを示す。

式(157)の目的は、ground-truthスコア関数へのアクセスに依存しており、これは自然画像をモデル化するような複雑な分布では利用できないことに注意してほしい。幸い、スコアマッチング[14, 15, 16, 17]として知られる代替技術は、ground-truthのスコアを知らなくてもこのFisherダイバージェンスを最小化するように導かれ、確率的勾配降下で最適化することができる。

まとめて、分布をスコア関数として表すことを学び、それを使ってランジュバン動力学などのMCMCの技術によりサンプルを生成することは、スコアベースの生成モデリング[9, 10, 11] として知られている。

バニラスコアマッチング（vanilla score matching）には、Song＆Ermon[9]が詳述しているように、3つの主要な問題がある。まず、スコア関数は高次元空間の低次元多様体に適用された場合、定義があいまいである。これは数学的に見ることができ、低次元多様体上にない点はすべて確率０となり、その対数は定義されない。これは、アンビエント空間全体の低次元多様体上にあることが知られている自然画像に対する生成モデルを学習しようとする場合に特に不都合である。

第二に、バニラスコアマッチングによって学習され推定されたスコア関数は、低密度領域では正確でない。このことは、式(157)で最小化する目的関数から明らかである。それは $p(x)$ 上の期待値であり、明示的にそこからのサンプルで訓練されるので、モデルはほとんど見られないか未見のサンプルに対して正確な学習シグナルを受け取らないであろう。これは、我々のサンプリング戦略では、高次元空間のランダムな位置（ランダムノイズである可能性が高い）から出発し、学習されたスコア関数に従って移動することになるので、問題である。ノイズの多い、あるいは不正確なスコア推定に従うため、最終的に生成されるサンプルも最適でない可能性があり、正確な出力に収束するためにさらに多くのイタレーションを必要とします。

最後に、ランジュバン動力学サンプリングは、たとえground-truthスコアを用いたとしても、混合しない可能性がある。真のデータ分布が2つの不連続な分布の混合物であるとする。

$p(x) = c_1 p_1(x) + c_2 p_2(x) \tag{159}$

次に、スコアが計算されるとき、log演算が分布から係数を分割し、勾配演算がそれをゼロにするので、これらの混合係数は失われる。これを視覚化するために、図6右に示すground-truthスコア関数は、3つの分布間の異なる重みに関係ないことに注意してほしい。描かれた初期化点からサンプリングするランジュバン動力学は、実際の混合ガウス分布では右下のモードが高い重みを持っているにもかかわらず、それぞれのモードに到達するチャンスがほぼ同じである。

この3つの欠点は、データに複数レベルのガウスノイズを加えることで、同時に解決できることがわかった。第一に、ガウスノイズ分布のサポートは空間全体であるため、摂動されたデータサンプルはもはや低次元の多様体に限定されることはない。次に、大きなガウスノイズを加えることで、各モードがデータ分布に占める面積が大きくなり、低密度の領域でより多くの学習信号が追加されます。最後に、分散を大きくした複数レベルのガウスノイズを加えることで、ground-truthの混合係数に対する中間的な分布になる。

形式的には、ノイズレベル $\left\{ \sigma_t \right\}_{t=1}^T$ の正の列を選び、漸次的に摂動されたデータ分布の系列を定義することができる。

$p_{\sigma_t} (x_t) = \int p(x) \mathcal{N} (x_t; x, \sigma_t^2 \boldsymbol{\rm{I}} ) dx \tag{160}$

そして、スコアマッチングを用いて、すべてのノイズレベルに対して同時にスコア関数を学習するニューラルネットワーク $s_{\theta}(x,t)$ を学習する。

$\arg \min_{\theta} \sum_{t=1}^T \lambda (t) \mathbb{E}_{p_{\sigma_t} (x_t)} \left[ \left|| s_{\theta} (x, t) - \nabla \log p_{\sigma_t}(x_t) \right||^2_2 \right] \tag{161}$

ここで $λ(t)$ はノイズレベル $t$ を条件とする正の重み付け関数である。この目的関数は、変分拡散モデルを学習するために式(148)で導かれた目的関数とほぼ一致することに注意されたい。さらに、著者らは生成手続きとして、アニールされたランジュバン動力学サンプリングを提案している。これは、各 $T,T-1, \ldots ,2,1$ について順にランジュバン動力学を実行することによりサンプルを生成するものである。初期化は固定された事前分布（例えば一様分布）から選択され、続く各サンプリングステップは前回のシミュレーションの最終サンプルから開始されます。ノイズレベルは時間ステップ $t$ の間に着実に減少し、時間ステップのサイズを小さくしていくので、サンプルは最終的に真のモードに収束していきます。これは、変分拡散モデルのマルコフ型HVAEの解釈で行われるサンプリング手順（ランダムに初期化されたデータベクトルが、減少するノイズレベル上で反復的に改良される）に直接類似している。

したがって、変分拡散モデルとスコアベース生成モデルの間には、その学習目的とサンプリング手順の両方において、明確な関連が確立されている。

一つは、拡散モデルを無限のタイムステップに自然に一般化するにはどうしたらいいかという問題である。マルコフ型HVAEでは、階層数を無限大 $T→∞$ に拡張すると解釈できる。このことは、同等のスコアベース生成モデルの観点から表現するとより明確である。無限大のノイズスケールの下では、連続時間における画像の摂動は確率過程として表現でき、したがって確率微分方程式（SDE）で記述できる。サンプリングはSDEを反転することで行われ、当然ながら各連続値ノイズレベルにおけるスコア関数を推定する必要がある[10]。SDEの異なるパラメタリゼーションは本質的に異なる摂動スキームを時間経過とともに記述し、ノイズ処理手順の柔軟なモデリングを可能にする[6]。

Guidance

これまで、我々はデータ分布 $p(x)$ のみをモデル化することに焦点をあててきた。しかし、条件付き分布 $p(x|y)$ の学習にもしばしば関心があり、条件付け情報 $y$ によって生成されるデータを明示的に制御することができるようになる。これは、カスケード拡散モデル（Cascaded Diffusion Models）[18]などの画像超解像モデルや、DALL-E 2[19] やImagen[7] などの最先端の画像テキストモデルのバックボーンを形成する。

条件情報を追加する自然な方法は、各反復においてタイムステップ情報を並べるだけである。式(32)の同時分布を思い出してほしい。

$p(x_{0:T}) = p(x_T) \prod_{t=1}^T p_{\theta} (x_{t-1} | x_t )$

そして、これを条件付き拡散モデルにするには、各遷移ステップで任意の条件付け情報 $y$ を追加するだけでよく、次のようになる。

$p(x_{0:T} | y) = p(x_T) \prod_{t=1}^T p_{\theta} (x_{t-1} | x_t , y ) \tag{162}$

例えば、 $y$ は画像テキスト生成におけるテキスト符号化であったり、超解像処理を行うための低解像度画像であったりする。このように、VDMのコアとなるニューラルネットワークは、従来通り、各解釈・実装に対して、 $\hat{x}_{\theta} (x_t, t, y) \approx x_0, \hat{\epsilon}_ {\theta} (x_t, t, y) \approx \epsilon_ 0, \ \rm{or} \ s_{\theta} (x_t, t, y) \approx \nabla \log p(x_t | y)$ と予測して学習することが可能である。

このバニラ定式化の注意点は、この方法で訓練された条件付き拡散モデルは、与えられた条件付け情報を無視したり、軽視したりするようになる可能性があるということである。そこで、サンプルの多様性を犠牲にして，モデルが条件付け情報に与える重みの量をより明示的に制御する方法として，誘導（Guidance）が提案されています。最も一般的な誘導は，分類器誘導（Classifier Guidance） [10, 20] と分類器放棄誘導（Classifier-Free Guidance） [21] の2つである。

Classifier Guidance

ここで、我々の目標は、任意のノイズレベル $t$ において、条件付きモデルのスコアである $\nabla \log p(x_t|y)$ を学習することであるとする。ここで、 $\nabla$ は簡潔さのために $\nabla_{x_t}$ の省略形であることを想起してほしい。ベイズの定理により、以下の等価形式を導出することができる。

$\begin{align} \nabla \log p(x_t | y) &= \nabla \log \left( \frac{p(x_t)p(y|x_t)}{p(y)} \right) \tag{163} \\ &= \nabla \log p(x_t) + \nabla \log p(y | x_t) - \nabla \log p(y) \tag{164} \\ &= \nabla \log p(x_t) + \nabla \log p(y|x_t) \tag{165} \end{align}$

ここで、 $\log p(y)$ の $x_t$ に対する勾配が0であることを利用している。

最終的に得られた結果は、条件付けられないスコア関数と分類器 $p(y|x_t)$ の逆勾配を組み合わせた学習と解釈することができる。したがって、分類器誘導[10, 20]では、任意のノイズ $x_t$ を取り込み、条件付き情報 $y$ を予測しようとする分類器とともに、先に導いたように条件付けられない拡散モデルのスコアが学習されることになる。そして、サンプリング処理中に、アニールされたランジュバン動力学に使用されるオーバーオール条件付きスコア関数が、条件づけられないスコア関数とノイズの多い分類器の逆勾配の和として計算される。

条件付き情報を考慮することをモデルに奨励または抑制するような、きめの細かいコントロールを導入するために、分類器誘導はハイパーパラメータ項 $γ$ でノイジーな分類器の逆勾配をスケールする。分類器誘導のもとで学習されたスコア関数は以下のようにまとめられる。

$\nabla \log p(x_t | y) = \nabla \log p(x_t) + \gamma \nabla \log p(y|x_t) \tag{166}$

直感的には、 $γ=0$ のとき、条件付き拡散モデルは条件付け情報を完全に無視することを学習し、 $γ$ が大きいとき、条件付き拡散モデルは条件付け情報に大きく依存するサンプルを生成するように学習する。この場合、ノイズが多い場合でも、与えられた条件情報を再生成しやすいデータしか生成しないため、サンプルの多様性が犠牲になる。

分類器誘導の欠点として、別途学習した分類器に依存することが挙げられます。分類器は任意にノイズの多い入力を扱わなければならず、既存の事前学習済み分類モデルのほとんどは最適化されていないため、拡散モデルと並行してアドホックに学習させる必要があります。

Classifier-Free Guidance

分類器放棄誘導（Classifier-Free Guidance）[21]では、条件付けられない拡散モデルと条件付き拡散モデルを用いて別の分類器モデルを学習することを放棄している。分類器放棄誘導におけるスコア関数を導出するために、まず、式(165)を変形し、以下のように示すことができる。

$\nabla \log p(y|x_t) = \nabla \log p(x_t | y) - \nabla \log p(x_t) \tag{167}$

そして、これを式(166)に代入すると、次のようになる。

$\begin{align} \nabla \log p(x_t | y) &= \nabla \log p (x_t) + \gamma \left( \nabla \log p(x_t | y) - \nabla \log p(x_t) \right) \tag{168} \\ &= \nabla \log p(x_t) + \gamma \log p(x_t | y) - \gamma \nabla \log p(x_t) \tag{169} \\ &= \gamma \nabla \log p (x_t | y ) + (1- \gamma) \nabla \log p (x_t) \tag{170} \end{align}$

繰り返しになるが、 $γ$ は学習した条件付きモデルが条件付け情報をどの程度気にするかを制御する項である。 $γ= 0$ のとき、学習済み条件付きモデルは条件付けを完全に無視し、条件付けられない拡散モデルを学習する。 $γ= 1$ のとき、モデルは明示的にバニラ条件分布を学習し、誘導は行わない。また、 $γ>1$ のとき、拡散モデルは条件付きスコア関数を優先させるだけでなく、無条件スコア関数から離れる方向に動く。つまり、条件情報を用いないサンプルの生成確率を下げ、条件情報を明示的に用いるサンプルを優先させる。これはまた、条件付け情報に正確に一致するサンプルを生成する代償として、サンプルの多様性を減少させる効果がある。

2つの別々の拡散モデルを学習することは高価であるので、我々は条件付き拡散モデルと条件付けられない拡散モデルの両方を特異条件付きモデルとして一緒に学習することが可能である。条件付け情報をゼロなどの固定定数に置き換えることで、条件づけられない拡散モデルを照会することができる。これは、本質的に、条件付け情報に対してランダムドロップアウトを実行することである。分類器放棄誘導は、条件付き生成の手順をより細かく制御できる一方で、特異な拡散モデルの訓練以上のものを必要としないため、エレガントである。

Closing

ここで、我々の研究過程で得られた知見を再掲する。まず、マルコフ型階層変分オートエンコーダの特殊なケースとして変分拡散モデルを導出し、3つの重要な仮定によりELBOの計算とスケーラブルな最適化が可能であることを説明する。VDMの最適化は、三つの潜在的な目的関数の一つを予測するニューラルネットワークの学習に帰着することを証明する。その三つとは、任意のノイズ処理からの元のソース画像、任意のノイズ処理画像からの元のソースノイズ、任意のノイズレベルにおけるノイズ処理画像のスコア関数、のいずれかである。次に、スコア関数を学習することの意味を深く掘り下げ、スコアベース生成モデリングの観点と明示的に結びつける。最後に、拡散モデルを用いた条件付き分布の学習方法について説明する。

要約すると、拡散モデルは生成モデルとして驚くべき能力を示しており、実際、ImagenやDALL-E 2などのテキスト条件付き画像生成に関する現在の最先端モデルで威力を発揮している。さらに、これらのモデルを可能にする数学は、非常にエレガントである。しかし、まだいくつかの欠点が残っている。

この手法は、私たち人間が、自然にデータをモデリングし、生成する方法とは思えない。我々は、何度もノイズを除去するランダムノイズとしてサンプルを生成しない。
VDMは解釈可能な潜在能力を生成しない。VAEではエンコーダの最適化により構造化潜在空間を学習するが、VDMでは各タイムステップのエンコーダは既に線形ガウスモデルとして与えられており、柔軟に最適化することはできない。したがって、中間潜在変数は、元の入力のノイズの多いバージョンに過ぎないものに制限される。
潜在変数は元入力と同じ次元に制限され、意味のある圧縮された潜在量構造を学習する努力をさらに怠らせることになる。
サンプリングは、両方の定式化の下で複数のノイズ除去ステップを実行しなければならないため、高価な手順である。仮定の1つに、最終的な潜在が完全にガウスノイズであることを保証するために、十分な数のタイムステップ $T$ を選択することを思いだして欲しい。サンプリングの際には、これらのタイムステップをすべて繰り返し、サンプルを生成する必要がある。

最後に、拡散モデルの成功は、生成モデルとしての階層VAEを強調するものである。我々は、エンコーダが些細で、潜在次元が固定され、マルコフ遷移が仮定されている場合でも、無限の潜在階層に一般化すると、データの強力なモデルを学習することができることを明らかにした。このことは、複雑なエンコーダと意味的に意味のある潜在空間を学習できる可能性のある、一般的な深いHVAEの場合に、さらなる性能向上が達成できることを示唆している。

謝辞：この研究のドラフトを見直し、多くの有益な編集とコメントを提供してくれたJosh Dillon、Yang Song、Durk Kingma、Ben Poole、Jonathan Ho、Yiding Jiang、Ting Chen、Jeremy CohenそしてChen Sunに感謝したい。本当にありがとう！

Reference

[7] Chitwan Saharia, William Chan, Saurabh Saxena, Lala Li, Jay Whang, Emily Denton, Seyed Kamyar SeyedGhasemipour, Burcu Karagol Ayan, S Sara Mahdavi, Rapha Gontijo Lopes, et al. Photorealistic text-to-image diffusion models with deep language understanding.arXivpreprintarXiv:2205.11487, 2022.

[8] Bradley Efron. Tweedie’s formula and selection bias. Journal of the American Statistical Association, 106(496):1602–1614, 2011.

[9] Yang Song and Stefano Ermon. Generative modeling by estimating gradients of the data distribution. Advances in Neural Information Processing Systems, 32, 2019.

[10] Yang Song, Jascha Sohl-Dickstein, Diederik P Kingma, Abhishek Kumar, Stefano Ermon, and Ben Poole. Score-based generative modeling through stochastic differential equations. arXiv preprint arXiv:2011.13456, 2020.

[11] Yang Song and Stefano Ermon. Improved techniques for training score-based generative models. Advances in neural information processing systems, 33:12438–12448, 2020.

[12] Yann LeCun, Sumit Chopra, Raia Hadsell, M Ranzato, and F Huang. A tutorial on energy-based learning. Predicting structured data, 1(0), 2006.

[13] Yang Song and Diederik P Kingma. How to train your energy-based models. arXiv preprint arXiv:2101.03288,2021.

[14] Aapo Hyvärinen and Peter Dayan. Estimation of non-normalized statistical models by score matching. Journal of Machine Learning Research, 6(4), 2005.

[15] Saeed Saremi, Arash Mehrjou, Bernhard Schölkopf, and Aapo Hyvärinen. Deep energy estimator networks. arXiv preprint arXiv:1805.08306, 2018.

[16] Yang Song, Sahaj Garg, Jiaxin Shi, and Stefano Ermon. Sliced score matching: A scalable approach to density and score estimation. In Uncertainty in Artificial Intelligence, pages 574–584. PMLR, 2020.

[17] Pascal Vincent. A connection between score matching and denoising autoencoders. Neural computation, 23(7):1661–1674, 2011.

[18] Jonathan Ho, Chitwan Saharia, William Chan, David J Fleet, Mohammad Norouzi, and Tim Salimans. Cascaded diffusion models for high fidelity image generation. J.Mach.Learn.Res., 23:47–1, 2022.

[19] Aditya Ramesh, Prafulla Dhariwal, Alex Nichol, Casey Chu, and Mark Chen. Hierarchical text-conditional image generation with clip latents. arXiv preprint arXiv:2204.06125, 2022.

[20] Prafulla Dhariwal and Alexander Nichol. Diffusion models beat gans on image synthesis. Advances in Neural Information Processing Systems, 34:8780–8794, 2021.

[21] Jonathan Ho and Tim Salimans. Classifier-free diffusion guidance. In NeurIPS 2021 Workshop on Deep Generative Models and Downstream Applications, 2021.