現在、ディープラーニングのエキサイティングなアプリケーションのほとんどを動かしている基盤モデルは、ほとんど例外なくTransformerアーキテクチャとそのコアとなるアテンションモジュールに基づいている。線形アテンション、ゲート付き畳み込み、再帰的モデル、構造化状態空間モデル（SSM）など、多くの二次時間以下のアーキテクチャが、長いシーケンスにおけるTransformerの計算効率の悪さに対処するために開発されてきたが、言語などの重要なモダリティではアテンションほどの性能を発揮していない。
我々は、このようなモデルの重要な弱点が、内容ベースの推論ができないことであることを明らかにし、いくつかの改善を行う。第一に、単にSSMパラメータを入力の関数とすることで、離散的なモダリティに対する弱点に対処し、現在のトークンに応じてシーケンスの長さ次元に沿って選択的に情報を伝搬したり、忘れたりすることを可能にする。第二に、この変更により効率的な畳み込みが使えなくなっても、リカレントモードでハードウェアを意識した並列アルゴリズムを設計する。これらの選択的SSMを、アテンションやMLPブロックさえも持たない単純化されたエンド・ツー・エンドのニューラルネットワークアーキテクチャ（Mamba）に統合する。
Mambaは、高速な推論（Transformerより5倍高いスループット）とシーケンス長における線形スケーリングを享受し、その性能は実データにおいて100万長シーケンスまで向上する。一般的な配列モデルのバックボーンとして、Mambaは言語、オーディオ、ゲノミクスなど様々なモダリティにおいて最先端の性能を達成している。言語モデリングにおいて、我々のMamba-3Bモデルは同じサイズのTransformerを上回り、事前学習と下流タスクでの評価の両方で2倍のサイズのTransformerに匹敵する。

1. Introduction

基盤モデル（FM）、すなわち膨大なデータで事前学習された後、下流のタスクに適応される大規模モデルは、現代の機械学習における効果的なパラダイムとして台頭してきた。これらのFMのバックボーンは多くの場合シーケンスモデルであり、言語、画像、音声、時系列、ゲノムなど様々な領域からの入力の任意のシーケンスで動作する（Brown et al. 2020; Dosovitskiy et al. 2020; Ismail Fawaz et al. 2019; Oord et al. 2016; Poli et al. 2023; Sutskever, Vinyals, and Quoc V Le 2014）。このコンセプトはモデルアーキテクチャの特定の選択に不可知論的であるが、現代のFMは主に単一のタイプのシーケンスモデル、すなわちTransformer（Vaswani et al. 2017）とそのコアとなるアテンション層（Bahdanau, Cho, and Bengio 2015）に基づいている。セルフアテンションの有効性は、コンテキストウィンドウ内で情報を高密度にルーティングする能力に起因し、複雑なデータをモデル化することを可能にする。しかし、この特性は、有限のウィンドウの外側のものをモデル化することができないこと、ウィンドウの長さに関して2次スケーリングすること、といった基本的な欠点をもたらす。これらの欠点を克服するために、より効率的なアテンションの変種に関する膨大な研究が登場している（Tay, Dehghani, Bahri, et al. 2022）。今のところ、これらの変種はいずれも、経験的に、領域横断的なスケールで有効であることが示されていない。

最近、構造化状態空間シーケンスモデル（SSM）（Gu, Goel, and Ré 2022; Gu, Johnson, Goel, et al. 2021）が、シーケンスモデリングのための有望なアーキテクチャのクラスとして出現した。これらのモデルは、古典的な状態空間モデル（Kalman 1960）から着想を得て、リカレントニューラルネットワーク（RNN）と畳み込みニューラルネットワーク（CNN）を組み合わせたものと解釈できる。このクラスのモデルは、再帰または畳み込みとして非常に効率的に計算でき、シーケンスの長さに対して線形または線形に近いスケーリングが可能である。さらに、特定のデータモダリティにおける長距離依存性（Gu, Dao, et al. 2020）をモデル化するための原理的なメカニズムを持っており、Long Range Arena（Tay, Dehghani, Abnar, et al. 2021）などのベンチマークを支配してきた。多くのSSM（Gu, Goel, and Ré 2022; Gu, Gupta, and Berant 2022; Y. Li et al. 2023; Smith, Warrington, and Linderman 2023)は、音声や視覚のような連続的な信号データを含む領域では成功を収めている(Goel et al. 2022; Nguyen, Goel, et al. 2022; Saon, Gupta, and Cui 2023)。しかし、テキストのような離散的で情報密度の高いデータのモデル化にはあまり有効ではない。

我々は、いくつかの軸で先行研究を改善し、シーケンスの長さを線形にスケーリングしながらTransformerのモデリング能力を達成する、新しいクラスの選択的状態空間モデルを提案する。

選択メカニズム まず、先行モデルの重要な限界、すなわち、入力に依存した方法でデータを効率的に選択する能力（すなわち、特定の入力に焦点を当てたり、無視したりする能力）を明らかにする。選択的コピーやインダクションヘッドのような重要な合成タスクに基づく直観を基に、入力に基づいてSSMパラメータをパラメータ化することで、簡単な選択メカニズムを設計する。これにより、モデルは無関係な情報をフィルタリングし、関連する情報を無期限に記憶することができる。

ハードウェアを意識したアルゴリズム この単純な変更は、モデルの計算に技術的な課題をもたらす。実際、先行するすべてのSSMモデルは、計算効率を上げるために、時間と入力に不変でなければならない。我々は、畳み込みの代わりにスキャンを使用してモデルを再帰的に計算するハードウェアを意識したアルゴリズムでこれを克服するが、GPUメモリ階層の異なるレベル間のIOアクセスを回避するために、展開された状態を実体化しない。その結果、理論的にも（すべての畳み込みベースのSSMの擬似線形と比較して、シーケンス長で線形にスケーリングする）、最新のハードウェア上でも（A100 GPUで最大3倍高速）、以前の方法よりも高速な実装が可能となった。

アーキテクチャ 先行するSSMアーキテクチャ（Dao, Fu, Saab, et al. 2023）の設計とTransformerのMLPブロックを1つのブロックに組み合わせることで、先行するディープシーケンスモデルアーキテクチャを簡素化し、選択的状態空間を組み込んだシンプルで均質なアーキテクチャ設計（Mamba）を導く。

選択的SSM、ひいてはMambaアーキテクチャは、シーケンス上で動作する一般的な基礎モデルのバックボーンとして適した、重要な特性を持つ完全リカレントモデルである。(i) 高品質：選択性は、言語やゲノミクスのような高密度なモダリティにおいて強力な性能をもたらす。(ii) 高速な学習と推論：学習中の計算とメモリはシーケンス長に対して線形にスケールし、推論中のモデルの自己回帰的なアンロールは、前の要素のキャッシュを必要としないため、ステップごとに一定の時間しか必要としない。(iii) 長い文脈：品質と効率性を合わせると、シーケンス長1Mまでの実データで性能向上が得られる。

我々は、一般的なシーケンスFMのバックボーンとしてのMambaの可能性を、いくつかのタイプのモダリティと設定において、事前学習の品質とドメイン固有のタスク性能の両方において実証的に検証する：

合成。大規模言語モデルの鍵として提案されているコピーや帰納法のような重要な合成タスクにおいて、Mambaはそれらを簡単に解くだけでなく、無限に長い（>1Mトークン）解を外挿することができる。
オーディオとゲノミクス。Mambaは、音声波形やDNA配列のモデリングにおいて、SaShiMi、Hyena、Transformersなどの先行する最先端モデルを、事前学習の品質とダウンストリームメトリクスの両方で上回っている（例えば、困難な音声生成データセットのFIDを半分以下に削減）。どちらの設定においても、100万長シーケンスまでの長いコンテキストで性能が向上している。
言語モデリング。Mambaは、Transformerに匹敵する性能を達成した最初の線形時間シーケンスモデルである。1Bパラメータまでのスケーリング則により、LLaMa（Touvron et al. 2023）に基づく非常に強力な最新のTransformerトレーニングレシピを含む、広範囲のベースラインの性能をMambaが上回ることを示す。私たちのMamba言語モデルは、同規模のTransformerと比較して5倍の生成スループットを持ち、Mamba-3Bの品質は2倍のサイズのTransformerに匹敵する（例えば、Pythia-3Bと比較して常識的推論で平均4ポイント高く、さらにPythia-7Bを上回る）。

モデルコードと事前学習済みチェックポイントは以下のサイトGitHub - state-spaces/mambaでオープンソース化されている。

2. State Space Models

構造化状態空間シーケンスモデル（S4）は、RNN、CNN、および古典的な状態空間モデルに広く関連する、深層学習のためのシーケンスモデルの最近のクラスである。具体的には、S4モデルは4つのパラメータ $( \Delta, A, B, C )$ で定義され、2段階でシーケンスからシーケンスへの変換を定義する。

離散化。第一段階は、 $\bar{A} = f_{A} (\Delta, A )$ と $\bar{B} = f_{B} (\Delta, A, B )$ という固定式によって、「連続パラメータ」 $(\Delta, A, B)$ を「離散パラメータ」 $(\bar{A}, \bar{B})$ に変換する。ここで、 $(f_{A}, f_{B} )$ の組を離散化規則と呼ぶ。式(4)で定義されるゼロ次ホールド(ZOH)など、様々なルールを使用することができる。

離散化には連続時間システムとの深いつながりがあり、解像度不変性（Nguyen, Goel, et al. 2022）や、モデルが適切に正規化されていることを自動的に保証する（Gu, Johnson, Timalsina, et al. 2023; Orvieto et al. 2023）といった付加的な特性を持たせることができる。また、RNNのゲーティング機構（Gu, Gulcehre, et al. 2020; Tallec and Ollivier 2018）にも関連しており、これについてはセクション3.5で再確認する。しかし、機械的な観点からは、離散化は単にSSMのフォワードパスにおける計算グラフの最初のステップとみなすことができる。別のタイプのSSMは、離散化ステップをバイパスし、代わりに $( \bar{A}, \bar{B} )$ を直接パラメータ化することができる(Zhang et al. 2023)。

計算。パラメータが $(\Delta, A, B, C) ↦ (\bar{A}, \bar{B}, C)$ と変換された後、モデルは線形再帰(2)またはグローバル畳み込み(3)の2つの方法で計算することができる。一般的に、このモデルは、並列化可能な効率的な学習（入力シーケンス全体が先読みされる）のために畳み込みモード(3)を使用し、効率的な自己回帰推論（入力が一度に1タイムステップずつ見られる）のためにリカレントモード(2)に切り替えられる。

線形時間不変性（LTI）。式(1)～(3)の重要な特性は、モデルのダイナミクスが時間を通して一定であることである。言い換えれば、 $(\Delta, A, B, C)$ 、ひいては $(\bar{A}, \bar{B})$ はすべてのタイムステップで固定される。この性質は線形時間不変性（LTI）と呼ばれ、再帰や畳み込みと深く関係している。非公式には、LTI SSMは線形再帰(2a)や畳み込み(3b)と等価であると考え、これらのクラスのモデルの総称としてLTIを用いる。

これまでのところ、全ての構造化SSMは、セクション3.3で議論する基本的な効率性の制約から、LTIであった（例えば、畳み込みとして計算された）。しかし、この研究の核となる洞察は、LTIモデルはある種のデータのモデリングにおいて基本的な制約があるということであり、我々の技術的な貢献は、効率のボトルネックを克服しながらLTI制約を取り除くことにある。

構造と次元。最後に、構造化SSMは、効率的に計算するためには $A$ 行列に構造を課す必要があるため、このような名前になっていることに注意する。最も一般的な構造は対角構造であり（Gu, Gupta, et al. 2022; Gupta, Gu, and Berant 2022; Smith, Warrington, and Linderman 2023）、我々もこれを用いる。

この場合、 $A \in \mathbb{R}^{N \times N}, B \in \mathbb{R}^{N \times 1}, C \in \mathbb{R}^{1 \times N}$ はすべて $N$ 個の数字で表現できる。バッチサイズ $B$ 、長さ $L$ 、 $D$ チャンネルの入力シーケンス $x$ を操作するために、SSM は各チャンネルに独立に適用される。この場合、全隠れ状態は入力ごとに $DN$ の次元を持ち、それをシーケンス長に渡って計算するには $O(BLDN)$ の時間とメモリが必要であることに注意されたい。これがセクション3.3で扱った根本的な効率性のボトルネックの根源である。

一般的な状態空間モデル。状態空間モデルという用語は非常に広い意味を持ち、単に潜在的な状態を持つ任意のリカレント過程の概念を表すことに注意する。マルコフ決定過程（MDP）（強化学習（Hafner et al. 2020））、動的因果モデリング（DCM）（計算論的神経科学（Friston, Harrison, and Penny 2003））、カルマンフィルター（制御（Kalman 1960））、隠れマルコフモデル（HMM）と線形力学システム（LDS）（機械学習）、リカレント（時には畳み込み）モデル（ディープラーニング）など、様々な分野で多くの異なる概念を指すために使われてきた。

本稿全体を通して、我々は「SSM」という用語を、構造化SSMまたはS4モデル（Gu, Goel, and Ré 2022; Gu, Gupta, et al. 2022; Gupta, Gu, and Berant 2022; Hasani et al. 2023; Ma et al. 2023; Smith, Warrington, and Linderman 2023）を指すものとして使用し、これらの用語を互換的に使用する。便宜上、線形回帰や大域的畳み込みの視点に焦点を当てたもの（Y. Li et al. 2023; Orvieto et al. 2023; Poli et al. 2023）など、このようなモデルの派生モデルも含め、必要に応じてニュアンスを明確にする。

SSMのアーキテクチャ。SSMは、エンドツーエンドのニューラルネットワークアーキテクチャに組み込むことができる、独立した配列変換である。（我々はSSMアーキテクチャをSSNNと呼ぶこともあるが、これはCNNが線形畳み込み層に対するように、SSM層に対するものである）。最もよく知られたSSMアーキテクチャーをいくつか取り上げるが、その多くは我々の主要なベースラインにもなる。

線形アテンション（Katharopoulos et al. 2020）は、退化した線形SSMと見なすことができる、再帰を含むセルフアテンションの近似である。
H3 (Dao, Fu, Saab, et al. 2023)は、この再帰をS4を使うように一般化したもので、SSMを2つのゲート接続で挟んだアーキテクチャとみなすことができる（図3）。H3はまた、メインのSSM層の前に、標準的な局所畳み込みを挿入しており、これはシフトSSMとして枠組まれている。
Hyena（Poli et al. 2023）はH3と同じアーキテクチャを使っているが、S4層をMLPパラメータ化されたグローバル畳み込みに置き換えている（Romero et al. 2021）。
RetNet（Y. Sun et al. 2023）は、アーキテクチャに追加のゲートを追加し、より単純なSSMを使用することで、畳み込みの代わりにマルチヘッドアテンション（MHA）の変種を使用し、並列化可能な別の計算経路を可能にしている。
RWKV (B. Peng et al. 2023）は、別の線形アテンション近似（attention-free Transformer（S. Zhai et al. 2021））に基づいて言語モデリング用に設計された最近のRNNである。その主な「WKV」メカニズムはLTI再帰を含み、2つのSSMの比率と見なすことができる。

他の密接に関連するSSMとアーキテクチャーについては、拡張された関連研究（付録B）を参照されたい。我々は、特にS5（Smith, Warrington, and Linderman 2023）、QRNNB（radbury et al. 2016）、SRU（Lei et al. 2017）を、我々のコア選択的SSMと最も密接に関連する手法とみなす。

3. Selective State Space Models

我々は、合成タスクからの直感を用いて我々の選択メカニズムを動機付けし（セクション3.1）、次にこのメカニズムを状態空間モデルに組み込む方法を説明する（セクション3.2）。結果として得られる時変SSMは畳み込みを使用することができず、いかに効率的に計算するかという技術的課題を提示する。我々は、最新のハードウェアのメモリ階層を利用したハードウェアを意識したアルゴリズムでこれを克服する（セクション3.3）。次に、アテンションやMLPブロックを用いないシンプルなSSMアーキテクチャについて述べる（セクション3.4）。最後に、選択機構の付加的な性質について述べる（セクション3.5）。

3.1 Motivation: Selection as a Means of Compression

我々は、シーケンスモデリングの基本的な問題は、コンテキストをより小さな状態に圧縮することであると主張する。実際、この観点から、一般的なシーケンスモデルのトレードオフを見ることができる。例えば、アテンションは効果的であると同時に非効率的でもある。このことは、自己回帰推論がコンテキスト全体（すなわちKVキャッシュ）を明示的に保存する必要があり、Transformersの遅い線形時間推論と2次時間学習の直接の原因となっていることからもわかる。一方、リカレントモデルは有限の状態を持つため効率的であり、一定時間の推論と線形時間の学習を意味する。しかし、その有効性は、この状態がどれだけ文脈を圧縮しているかによって制限される。

この原理を理解するために、合成タスクの2つの実行例に注目する（図2）。

選択的コピータスクは、記憶するトークンの位置を変化させることで、一般的なコピータスク（Arjovsky, Shah, and Bengio 2016）を修正する。関連するトークン（色付き）を記憶し、無関係なトークン（白）をフィルタリングできるように、内容を認識した推論が必要である。
インダクション・ヘッドタスクは、LLMの文脈内学習能力の大部分を説明すると仮定された、よく知られたメカニズムである（Olsson et al. 2022）。この課題では、適切な文脈で正しい出力を出すタイミングを知るために、文脈を意識した推論が必要となる（黒）。

これらのタスクは、LTIモデルの失敗モードを明らかにしている。リカレントの観点からは、その一定のダイナミクス（例えば(2)の $\bar{A}, \bar{B}$ 遷移）は、文脈から正しい情報を選択することができず、入力に依存した方法でシーケンスに沿って渡される隠れた状態に影響を与えることができない。畳み込みの観点からは、グローバル畳み込みは、時間認識のみを必要とするため、バニラコピー課題（Romero et al.　2021）を解決できることが知られているが、選択的コピー課題（Selective Copying task）に対しては、内容認識がないため困難であることが知られている（図2）。より具体的には、入力と出力の間隔は変化するため、静的な畳み込みカーネルではモデル化できない。

要約すると、シーケンスモデルの効率と有効性のトレードオフは、どれだけ状態を圧縮するかによって特徴付けられる。効率的なモデルは小さな状態を持たなければならないが、有効なモデルはコンテキストから必要な情報をすべて含む状態を持たなければならない。そこで、シーケンスモデルを構築するための基本的な原理は、選択性、つまり、コンテクストを意識して、シーケンス状態への入力に焦点を当てたり、フィルタリングしたりする能力であることを提案する。特に、選択メカニズムは、情報がシーケンスの次元に沿ってどのように伝搬し、あるいは相互作用するかを制御する（詳細な議論についてはセクション3.5を参照）。

3.2 Improving SSMs with Selection

モデルに選択メカニズムを組み込む1つの方法は、シーケンスに沿った相互作用に影響を与えるパラメータ（RNNのリカレントダイナミクスやCNNの畳み込みカーネルなど）を入力依存にすることである。アルゴリズム1と2は、我々が使用する主な選択メカニズムを示している。主な違いは、単純にいくつかのパラメータ $\Delta, B, C$ を入力の関数とし、それに伴ってテンソルの形状を全体的に変化させることである。特に、これらのパラメータが長さ次元 $L$ を持つようになり、モデルが時不変から時変に変わったことを意味する。(形状の注釈はセクション2で説明した）。これは畳み込み(3)との等価性を失い、次に説明する効率に影響する。

私たちは、特に、 $\text{Linear}_{d}$ を $d$ 次元へのパラメータ化された投影として、 $s_{B} (x) = \text{Linear}_{N} (x)$ 、 $s_{C} (x) = \text{Linear}_{N} (x)$ 、 $s_{\Delta} (x) = \text{Broadcast}_{D} ( \text{Linear}_{1} (x) )$ 、 $\tau_{\Delta} = \text{softplus}$ を選択した。

𝑠と∆の選択は、セクション3.5で説明したRNNのゲーティング機構との関連によるものである。 $s_{\Delta}$ と $\tau_{\Delta}$ の選択は、セクション3.5で説明したRNNのゲーティングメカニズムに関連している。

3.3 Efficient Implementation of Selective SSMs

畳み込み（Krizhevsky, Sutskever, and Hinton 2012）やTransformer (Vaswani et al. 2017) のような、ハードウェアフレンドリーなアーキテクチャは、幅広いアプリケーションで利用されている。ここでは、選択的SSMを最新のハードウェア（GPU）上でも効率的にすることを目指す。選択メカニズムは極めて自然であり、以前の研究では、リカレントSSMにおいて $\Delta$ を時間的に変化させるなど、選択の特殊なケースを取り入れることを試みている（Gu, Dao, et al.）しかし、先に述べたように、SSMの使用における核心的な限界は計算効率であり、そのためS4とすべての派生研究は、LTI（非選択的）モデル、最も一般的にはグローバル畳み込みの形式を使用していた。

3.3.1 Motivation of Prior Models

まずこの動機を再検討し、先行手法の限界を克服するための我々のアプローチを概説する。

セクション3.1で議論したように、隠れ状態の次元が大きいモデルはより効果的であるが、より遅い。したがって、我々はスピードとメモリーのコストを支払うことなく、隠れ状態の次元を最大化したい。
後者(3)は前者(2)を展開することで得られるので、リカレント・モードは畳み込みモードよりも柔軟であることに注意する（Gu, Goel, and Ré 2022; Gu, Johnson, Goel, et al. 2021）。しかし、この場合、入力 $x$ と出力 $y$ の形状 $(B, L, D)$ よりもはるかに大きい（SSMの状態次元である、 $N$ のファクターにより)形状 $(B, L, D, N)$ を持つ潜在状態 $h$ を計算し、実体化する必要がある。そのため、状態計算をバイパスし、 $(B, L, D)$ だけの畳み込みカーネル(3a)を実現する、より効率的な畳み込みモードが導入された。
先行するLTI SSMは、リカレントと畳み込みの二重形式を活用することで、有効な状態次元を従来のRNNよりも遥かに大きい $N (\approx 10-100)$ のファクターだけ増加させることができ、効率性のペナルティはない。

3.3.2 Overview of Selective Scan: Hardware-Aware State Expansion

選択メカニズムはLTIモデルの限界を克服するように設計されている。同時に、SSMの計算問題を再検討する必要がある。我々は、カーネル融合、並列スキャン、再計算という3つの古典的手法でこれに対処する。我々は主に2つの観察を行う：

素朴なリカレント計算が $O(BLDN)$ FLOPsを使うのに対し、畳み込み計算は $O(BLD \log(L) )$ FLOPsであり、前者の方が定数係数が小さい。このように、シーケンスが長く、状態次元 $N$ がそれほど大きくない場合、リカレントモードの方が少ないFLOP数で済む。
2つの課題は、再帰のシーケンシャルな性質と、大きなメモリ使用量である。後者に対処するため、畳み込みモードと同様に、完全な状態 $h$ を実際に実体化しないようにすることができる。

主なアイデアは、最新のアクセラレータ（GPU）の特性を利用して、メモリ階層のより効率的なレベルでのみ状態 $h$ を実体化することである。特に、ほとんどの演算（行列の乗算を除く）は、メモリ帯域幅によって制限される (Dao, Fu, Ermon, et al. 2022; Ivanov et al. 2021; Williams, Waterman, and Patterson 2009）。これにスキャン演算も含まれ、カーネルフュージョンを使用してメモリIOの量を削減し、標準的な実装と比較して大幅な高速化を実現している。

具体的には、サイズ $(B, L, D, N)$ のスキャン入力 $(\bar{A}, \bar{B})$ をGPU HBM（高帯域幅メモリ）に準備する代わりに、SSMパラメータ $( \Delta, A, B, C )$ を低速HBMから直接ロードし、SRAMで離散化と再帰を実行し、サイズ $(B, L, D)$ の最終出力をHBMに書き戻す。

逐次再帰を回避するために、線形ではないにもかかわらず、作業効率の高い並列スキャンアルゴリズムで並列化できることを確認する（Blelloch 1990; Martin and Cundy 2018; Smith, Warrington, and Linderman 2023）。

最後に、バックプロパゲーションに必要な中間状態の保存も避けなければならない。中間状態は保存されず、入力がHBMからSRAMにロードされるバックワードパスで再計算される。その結果、融合された選択スキャン層は、FlashAttentionを使用した最適化されたトランスフォーマ実装と同じメモリ要件になる。

融合カーネルと再計算の詳細は付録Dにある。完全な選択SSMレイヤーとアルゴリズムを図1に示す。

3.4 A Simplified SSM Architecture

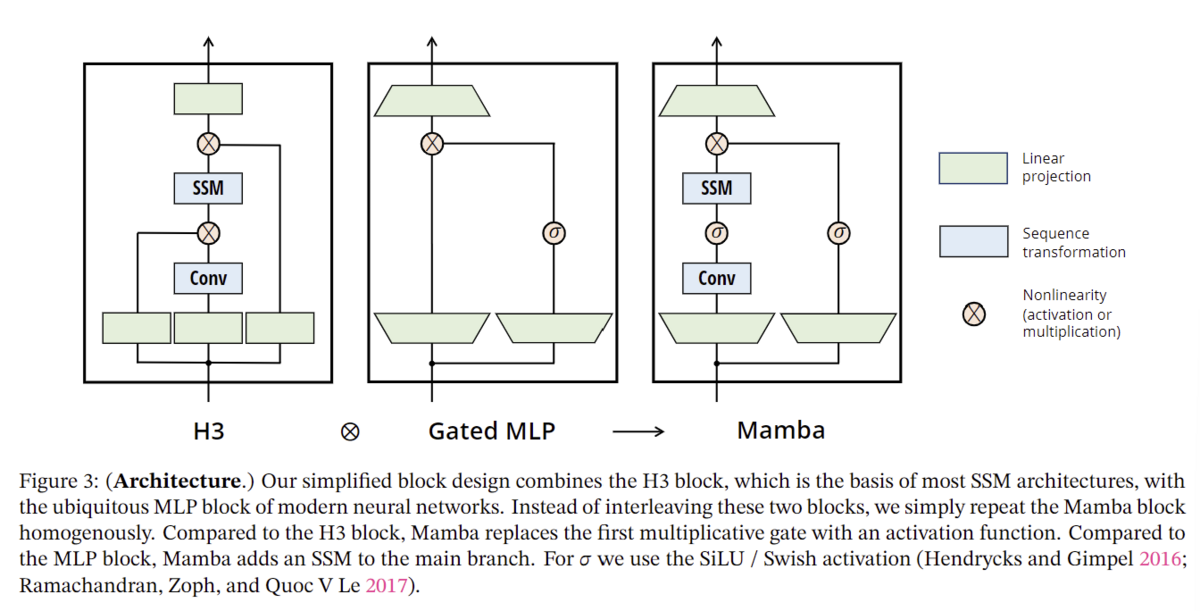
構造化SSMと同様に、選択的SSMはニューラルネットワークに柔軟に組み込むことができる独立したシーケンス変換である。H3アーキテクチャーは最もよく知られたSSMアーキテクチャー（セクション2）の基礎であり、一般に線形アテンションにヒントを得たブロックとMLP（多層パーセプトロン）ブロックから構成されている。我々はこの2つのコンポーネントを1つにまとめ、均質に積み重ねることで、このアーキテクチャを単純化している（図3）。これは、アテンションと似たようなことを行うGAU（gated attention unit）（Hua et al. 2022）から着想を得ている。

このアーキテクチャでは、モデルの次元 $D$ を制御可能な拡大係数 $E$ で拡大する。各ブロックについて、パラメータの大部分（ $3ED^2$ ）は線形投影（入力投影は $2ED^2$ 、出力投影は $ED^2$ ）にあり、内側のSSMの寄与は少ない。それに比べてSSMパラメータ（ $\Delta, B, C$ 、行列 $A$ に対する投影）の数はずっと少ない。このブロックを繰り返し、標準的な正規化と残差接続をインターリーブして、Mambaアーキテクチャを形成する。実験では常に $E=2$ に固定し、TransformerのインターリーブされたMHA（multi-head attention）とMLPブロックの $12D^2$ パラメータに合うように、ブロックの2つのスタックを使用する。我々はSiLU/Swish活性化関数（Hendrycks and Gimpel 2016; Ramachandran, Zoph, and Quoc V Le 2017）を使用し、Gated MLPが人気のある "SwiGLU "バリアント (Chowdhery et al. 2023; Shazeer 2020; Touvron et al. 2023）になるように動機づける。最後に、我々はオプションの正規化層（我々はLayerNorm （J. L. Ba, Kiros, and Hinton 2016）を選択）を追加で使用するが、RetNetも同じような場所で正規化層を使用している（Y. Sun et al. 2023）。

3.5 Properties of Selection Mechanisms

選択メカニズムは、より伝統的なRNNやCNN、異なるパラメータ（アルゴリズム2の $A$ など）、または異なる変換 $s(x)$ を使用するなど、さまざまな方法で適用できる、より広い概念である。

3.5.1 Connection to Gating Mechanisms

最も重要なコネクションを強調する。RNNの古典的なゲーティング機構は、SSMの選択機構のインスタンスである。RNNのゲーティングと連続時間システムの離散化との関連はよく確立されていることに注意する（Funahashi and Nakamura 1993; Tallec and Ollivier 2018）。実際、定理1はGu, Johnson, Goel, et al. （2021, Lemma 3.1）をZOH離散化と入力依存ゲートに一般化した改良である（証明は付録C）。より広義には、SSMにおける $\Delta$ は、RNNゲート機構の一般化された役割を果たすとみなすことができる。先行研究と同様に、SSMの離散化はヒューリスティックゲーティング機構の原理的基礎であるという見解を採用する。

セクション3.2で述べたように、 $s_{\Delta}, \tau_{\Delta}$ の具体的な選択はこの関連からである。特に、与えられた入力 $x_t$ が（合成タスクで必要なように）完全に無視されるべきであれば、すべての $D$ チャンネルはそれを無視すべきで、 $\Delta$ で繰り返し/ブロードキャストする前に、入力を1次元に投影する。

3.5.2 Interpretation of Selection Mechanisms

ここでは、選択のメカニズム的効果について、特に2つ詳しく説明する。

可変間隔。選択性によって、関心のある入力の間に発生する可能性のある無関係なノイズトークンをフィルタリングすることができる。これは「選択的コピー」タスクで例証されるが、一般的なデータモダリティ、特に離散データ、例えば「um」のような言語フィラーの存在などではどこにでも発生する。この性質は、例えばゲーテッドRNNの場合（定理1）の $g_t \to 0$ の時のように、モデルが機械的に特定の入力 $x_t$ をフィルタリングできるために生じる。

文脈のフィルタリング。より多くのコンテキストが厳密により良い性能につながるはずの原則にもかかわらず、多くのシーケンスモデルはコンテキストが長くなっても改善しないことが経験的に観察されている（F. Shi et al. 2023）直感的な例としては、大域畳み込み（および一般的なLTIモデル）がある。一方、選択的モデルはいつでも状態をリセットして余計な履歴を取り除くことができるので、原理的にはコンテキストの長さに応じて単調に性能が向上する（例えばセクション4.3.2）。

境界リセット。複数の独立したシーケンスがつなぎ合わされた設定では、Transformerは特定のアテンションマスクをインスタンス化することでそれらを分離しておくことができるが、LTIモデルはシーケンス間の情報を流出させる。選択的SSMは、境界で状態をリセットすることもできる（例えば、 $\Delta_t \to \infty$ や $g_t \to 1$ のときの定理1）。このような設定は、人為的に（例えば、ハードウェアの使用率を向上させるために文書をまとめて）、あるいは自然に（例えば、強化学習におけるエピソードの境界（Lu et al. 2023））発生する。

さらに、各選択パラメータの効果について詳しく説明する。

$\Delta$ の解釈。一般に、 $\Delta$ は、現在の入力 $x_t$ をどれだけ重視するか、無視するかのバランスを制御する。これはRNNゲート（例えば定理1の $g_t$ ）を一般化したもので、機械的には、大きな $\Delta$ は状態 $h$ をリセットし、現在の入力 $x$ に集中し、小さな $\Delta$ は状態を維持し、現在の入力を無視する。SSM(1)-(2)は、タイムステップ $\Delta$ で離散化された連続システムとして解釈することができ、この文脈では、大きな $\Delta \to \infty$ はシステムが現在の入力に長く集中する（したがって、入力を「選択」して現在の状態を忘れる）ことを表し、小さな $\Delta \to 0$ は過渡的な入力を無視することを表す。

$A$ の解釈 。パラメーター $A$ も選択的であり得るが、最終的には $\bar{A} = \exp (\Delta A)$ （離散化(4)）を介した $\Delta$ との相互作用を通じてのみモデルに影響を与えることに注意する。したがって、 $\Delta$ の選択性は $( \bar{A}, \bar{B} )$ の選択性を保証するのに十分であり、改善の主な原因である。我々は、 $\Delta$ に加えて（あるいは $\Delta$ の代わりに） $A$ を選択的にすることで、同様のパフォーマンスが得られると仮定し、簡単のため省く。

$B$ と $C$ の解釈。スモデルのコンテクストを効率的な状態に圧縮できるように、無関係な情報をフィルタリングすることである。SSMでは、 $B$ と $C$ を選択的に変更することで、入力 $x_t$ を状態 $t$ に入れるか、状態を出力 $t$ に入れるかをより細かく制御できる。これらは、モデルがそれぞれ内容（入力）と文脈（隠れた状態）に基づいてリカレント・ダイナミクスを調節できるようにすると解釈できる。

3.6 Additional Model Details

実数vs複素数。先行するSSMのほとんどは、状態 $h$ に複素数を用いており、これは多くのタスクで強力な性能を発揮するために必要である（Gu, Goel, and Ré 2022）。しかし、完全に実数値のSSMは問題なく動作するようであり、いくつかの設定においてはより良い可能性さえあることが経験的に観察されている（Ma et al. 2023）。複素数と実数のトレードオフは、データモダリティの連続-離散スペクトルに関連しており、連続モダリティ（音声、ビデオなど）には複素数が有効だが、離散モダリティ（テキスト、DNAなど）には複素数が有効ではないという仮説を立てた。

初期化。先行するSSMのほとんどは、特に複素数の場合の特別な初期化を提案している。複素数の場合のデフォルトの初期化はS4D-Linであり、実数の場合はHIPPO理論（Gu, Dao, et al. 2020）に基づくS4D-Real（Gu, Gupta, et al. 2022）である。これらは $A$ の $n$ 番目の要素をそれぞれ $-1/2 + ni$ と $-(n+1)$ と定義する。しかし、多くの初期化は、特に大データや実数値のSSM領域でうまくいくことが期待される。

$\Delta$ のパラメータ化。我々は $\Delta$ の選択的調整を $s_{\Delta}(x) = \text{Broadcast}_{D}(\text{Linear}_{1}(x) )$ と定義したが、これは $\Delta$ の力学（セクション3.5）に動機づけられたもので、1次元からより大きな次元 $R$ に一般化できることがわかる。我々はこれを $D$ の小数とし、ブロック内の主要な線形投影と比較して無視できる数のパラメータを使用する。さらに、ブロードキャスト操作は、1と0の特定のパターンに初期化された別の線形射影と見なすことができる。この射影が訓練可能であれば、これは低ランク射影と見なすことができる $s_{\Delta} (x) = \text{Linear}_{\Delta} (\text{Linear}_{R} (x))$ という代替につながる。

我々の実験では、SSMに関する先行研究（Gu, Johnson, Timalsina, et al. 2023）に従い、 $\Delta$ パラメータ（バイアス項とみなすことができる）は $\tau_{\Delta}^{-1}$ に初期化される。

備考3.1。我々の実験結果を簡潔にするため、選択的SSMをS6モデルと略すことがある。これは、選択メカニズムを持つS4モデルであり、スキャンで計算されるからである。

付録C：選択的SSMのメカニズム

定理1の証明。 $N=1$ 、 $A=-1$ 、 $B=1$ 、 $s_{\Delta} = \text{Linear} (x)$ 、 $\tau_{\Delta} = \text{softplus}$ とした際の選択的SSM（アルゴリズム 2）について考える。これに対応する連続時間SSM(1)は、以下であらわされ、これはリーキー積分器とも呼ばれる。

$\displaystyle \begin{align} h(t) = -h(t) + x(t) \end{align}$

離散化のステップサイズは、以下。

$\displaystyle \begin{align} \Delta_t &= \tau_{\Delta} ( \text{Parameter} + s_{\Delta} (x_t) ) \\ &= \text{softplus} ( \text{Parameter} + \text{Linear} (x_t) ) \\ &= \text{softplus} ( \text{Linear} (x_t) ) \end{align}$

ここで、パラメータは学習可能なバイアスとみなすことができ、線形射影に折り込まれることがわかる。ここで0次ホールド（ZOH）離散化公式を適用する：

$\displaystyle \begin{align} \bar{A}_t &= \exp (\Delta A ) = \frac{1}{1 + \exp (\text{Linear} ( x_t ) )} = \sigma ( - \text{Linear} ( x_t ) ) \\ &= 1- \sigma ( \text{Linear} (x\_t ) ) \\ \bar{B}_t &= ( \Delta A )^{-1} ( \exp ( \Delta A ) - I ) \cdot \Delta B = - ( \exp ( \Delta A ) - I ) = 1 - \bar{A} \\ &= \sigma ( \text{Linear} ( x_t ) ) \end{align}$

したがって、最終的な離散漸化式(2a)は、以下のように求められる。

$\displaystyle \begin{align} g_t = \sigma ( \text{Linear} (x_t) ) \\ h_t = ( 1- g_t ) h_{t-1} + g_t x_t \end{align}$

付録D：ハードウェアを意識した選択的SSMのためのアルゴリズム

入力依存の選択性がなければ、SSMはプリミティブとして高速フーリエ変換（FFT）を活用した畳み込みとして効率的に実装できる（Dao, Fu, Saab, et al. 2023; Gu, Goel, and Ré 2022）。選択性を持つSSMはもはや畳み込みと等価ではないが、並列連想スキャンを活用する。SSMスキャンは理論的には効率的だが（ $O(BLDN)$ FLOPs、 $L$ で線形スケーリング）、選択的SSMを用いた基礎モデルの学習には、最新のハードウェア（GPU）でも効率的であることが要求さる。本稿では、カーネル融合と再計算を用いてSSMスキャンを高速かつメモリ効率的に行う方法について述べる。セクション4.5で畳み込みやアテンションと比較した我々のスキャン実装の速度を評価し、シーケンス長32Kでアテンションより最大7倍高速であり、最高のアテンション実装（FlashAttention）と同等のメモリ効率であることを示す。

速度。最新のハードウェアアクセラレータ（GPU）では、ほとんどの演算（行列乗算を除く）はメモリ帯域幅によって制限される（Dao, Fu, Ermon, et al. 2022; Ivanov et al. 2021; Williams, Waterman, and Patterson 2009）。私たちのスキャン演算もこのケースに当てはまり、カーネルフュージョンを使用してメモリIOの量を削減し、標準的な実装と比較して大幅な高速化を実現している。

セクション3. 2 のスキャン・アルゴリズムの標準的な実装方法は、GPU HBM（high-bandwidth memory、一般に GPU メモリと呼ばれる）にサイズ $(B, L, D, N)$ のスキャン入力 $\bar{A}, \bar{B}$ を準備することで、並列連想スキャン実装を呼び出して、サイズ $(B, L, D)$ のスキャン出力を GPU HBM に書き込み、そのスキャン出力に $C$ を乗算してサイズ $(B, L, D)$ の出力を生成する。しかし、これには $O(BLDN)$ オーダーのメモリーの読み書きが必要である。代わりに、離散化ステップ、スキャン、 $C$ との乗算を1つのカーネルに融合することができる。

$O(BLD + DN)$ バイトのメモリ $(\Delta, A, B, C)$ を低速HBMから高速SRAMに読み込む。
離散化して、SRAMにサイズ $(B, L, D, N)$ の $\bar{A}, \bar{B}$ を生成。
並列連想スキャンを行い、SRAMにサイズ $(B, L, D, N)$ の中間状態を生成。
$C$ との乗算と和算を行い、サイズ $(B, L, D)$ の出力を生成し、HBMに書き込む。

このようにして、IOを $O(N)$ （状態の次元）のファクターだけ減らすことができ、実際には20～40倍高速化される（セクション4.5）。

シーケンスの長さが長すぎてSRAM（HBMよりはるかに小さい）に収まらない場合は、シーケンスをチャンクに分割し、各チャンクでフューズドスキャンを実行する。中間スキャン状態がある限り、次のチャンクでスキャンを続けることができる。

メモリ。古典的な再計算のテクニックを使って、選択的SSM層の学習に必要なメモリの総量を削減する方法を説明する。

フォワードパスの融合方法から、我々はメモリの爆発を避けるために、サイズ $(B, L, D, N)$ の中間状態を保存しない。しかし、これらの中間状態はバックワードパスで勾配を計算するために必要である。その代わりに、これらの中間状態をバックワードパスで再計算する。HBMからSRAMに読み出される入力 $\Delta, A, B, C$ と出力勾配は $O(BLN + DN)$ のサイズであり、入力勾配も $O(BLN + DN)$ であるため、再計算はHBMから $O(BLDN)$ 要素を読み出すコストを回避する。つまり、バックワードパスでSSM状態を再計算することで、それらを保存してHBMから読み出すよりも計算が高速化される。

スキャン操作だけのメモリ要件を最適化するだけでなく、選択的SSMブロック全体（入力投影、畳み込み、活性化、スキャン、出力投影）のメモリ要件を最適化するために再計算を使用する。特に、多くのメモリを消費するが再計算が速い中間活性化（活性化関数の出力や短い畳み込みなど）は保存しない。その結果、選択的SSM層は、FlashAttentionを用いた最適化されたTransformer実装と同じメモリ要件を持つ。特に、各アテンション層（FlashAttention）は1トークンあたり約12バイトの活性化を保存し、各MLP層は1トークンあたり約20バイトの活性化を保存し、合計32バイト（FP16またはBF16での混合精度学習を仮定）となる。各選択的SSMはトークンあたり約16バイトのアクティブを保存する。したがって、2層の選択的SSMは、アテンション層とMLP層とほぼ同じ活性化メモリを持つことになる。

4. Empirical Evaluation

セクション4.1では、セクション3.1で動機付けされた2つの合成タスクを解くMambaの能力をテストする。次に、3つの領域で評価を行い、それぞれ自己回帰の事前学習と下流タスクで評価する。

セクション4.2: 言語モデルの事前学習（スケーリング則）と、ゼロショットの下流評価。
セクション4.3： DNA配列の事前学習と、長い配列の分類タスクでの微調整。
セクション4.4: 音声波形の事前学習と、自己回帰的に生成された音声クリップの品質。

最後に、セクション4.5では学習時と推論時のMambaの計算効率を示し、セクション4.6ではアーキテクチャと選択的SSMの様々なコンポーネントを除去する。

4.1 Synthetic Tasks

タスクの詳細とトレーニングプロトコルを含む、これらのタスクに関する実験の詳細は付録E.1にある。

4.1.1 Selective Copying

コピータスクはシーケンスモデリングにおいて最もよく研究された合成タスクの一つであり、元々はリカレントモデルの記憶能力をテストするために設計された。セクション3.1で議論したように、LTIのSSM（線形リカレンスとグローバル畳み込み）は、データについて推論する代わりに、時間だけを追跡することで、このタスクを簡単に解くことができる。例えば、正確に正しい長さの畳み込みカーネルを構成することで行われる（図2）。これはグローバル畳み込みに関する以前の研究（Romero et al. 2021）。選択的コピー（Selective Copying）タスクは、トークン間の間隔をランダムにすることで、このショートカットを防ぐ。なお、このタスクは以前にDenoisingタスクとして紹介されている（Jing et al. 2019）。

多くの先行研究が、アーキテクチャゲーティング（乗法的相互作用）を追加することで、モデルに「データ依存性」を付与し、関連するタスクを解決できると主張している（Dao, Fu, Saab, et al. 2023; Poli et al. 2023）。しかし、このようなゲーティングはシーケンス軸に沿った相互作用がなく、トークン間の間隔に影響を与えることができないため、この説明は直感的には不十分だと思われる。特に、ゲーティングアーキテクチャは選択メカニズムの一例ではない（付録A）。

表1から、H3やMambaのようなゲーティングアーキテクチャは部分的にしか性能を向上させないが、選択メカニズム（S4をS6に変更する）は、特にこれらの強力なアーキテクチャと組み合わせた場合に、この課題を簡単に解決することが確認された。

4.1.2 Induction Heads

インダクションヘッド（Olsson et al. 2022）は、機械論的解釈可能性レンズ（Elhage et al. 2021）に基づく単純なタスクであり、LLMの文脈内学習能力を驚くほど予測する。例えば、モデルが「ハリー・ポッター」のようなビッグラムをシークエンスで見たことがある場合、次に同じシークエンスで「ハリー」が現れたとき、モデルは履歴からコピーすることで「ポッター」を予測できるはずである。

データセット。これはこのタスクに関する先行研究（Dao, Fu, Saab, et al. 2023）さらに、テスト時に $2^6 = 64$ から $2^{20} = 1048576$ までのシーケンス長の範囲で評価することで、汎化能力と外挿能力を調査した。

モデル。インダクションヘッドに関する確立された研究に従い、我々は2層モデルを使用し、これによりアテンションはインダクションヘッド課題を機械的に解くことができる（Olsson et al.2022）。マルチヘッドアテンション（8ヘッド、様々な位置エンコーディング）とSSMバリエーションの両方をテストする。モデル次元 $D$ はMambaでは64、他のモデルでは128を使用。

結果。表2から、Mamba、より正確にはその選択的SSM層は、関連するトークンを選択的に記憶し、その間にある他の全てを無視する能力を持つため、タスクを完璧に解く能力を持つことがわかる。他のどの手法も2倍を超えないのに対し、Mambaは100万長シーケンス、つまりトレーニング中に見た長さの4000倍の長さのシーケンスに対しても完璧に汎化する。

アテンションモデルの位置エンコーディングのバリエーションのうち、xPos（これは長さの外挿のために設計された）は他のものよりもわずかに優れている。また、メモリの制限のため、すべてのアテンションモデルはシーケンス長 $2^{14} = 16384$ までしかテストされていないことに注意。他のSSMのうち、H3とハイエナは、Poliら（2023）の所見に反して類似している。

4.2 Language Modeling

標準的な自己回帰言語モデリングに関するMambaアーキテクチャを、他のアーキテクチャと比較し、事前学習メトリクス（perpelxity）とゼロショット評価の両方で評価する。モデルサイズ（深さと幅）はGPT3の仕様を反映するように設定した。Pileデータセット（L. Gao, Biderman, et al. 2020）を用い、 Brownら（2020）の訓練方法に従った。すべてのトレーニングの詳細は付録E.2にある。

4.2.1 Scaling Laws

ベースラインとして、標準的なTransformerアーキテクチャ（GPT3アーキテクチャ）と、PaLMおよびLLaMaアーキテクチャ（Roatary Embedding、SwiGLU MLP、LayerNormの代わりにRMSNorm、線形バイアスなし、より高い学習率など）に基づく、我々が知っている最強のTransformerレシピ（ここではTransformer++と呼ぶ）と比較する。また、他の最近のサブ2次アーキテクチャとの比較も行っている（図4）。すべてのモデルの詳細は付録E.2にある。

図4は標準的なChinchilla（Hoffmann et al. 2022）プロトコルの下で、 $\approx 125M$ から $\approx 1.3B$ パラメータまでのモデルにおけるスケーリング則を示している。Mambaは、特にシーケンス長が長くなるにつれて、現在標準となっている非常に強力なTransformerレシピ（Transformer++）の性能に匹敵する最初のアテンションフリーモデルである。RWKVとRetNetのベースラインは、SSMとしても解釈可能な先行する強力なリカレントモデルであるが、効率的な実装がなされていないため、メモリ不足や非現実的な計算が必要となり、文脈長8kでの完全な結果が得られていない。

4.2.2 Downstream Evaluations

表3は、様々なダウンストリームのゼロショット評価タスクにおけるMambaのパフォーマンスを示している。最も重要なのはPythia (Biderman et al. 2023)とRWKV (B. Peng et al. 2023)であり、これらは我々のモデルと同じトークナイザー、データセット、学習長（300Bトークン）で学習されている。(ただし、MambaとPythiaは文脈長2048、RWKVは文脈長1024で学習している)。

4.3 DNA Modeling

大規模な言語モデルの成功に触発され、最近、基盤モデルのパラダイムをゲノミクスに利用しようという試みがなされている。DNAは、有限の語彙を持つ離散的なトークンのシーケンスから構成されているという点で、言語に例えられている。また、DNAは長距離の依存関係をモデル化する必要があることでも知られている（Avsec et al. 2021）。我々は、DNAの長鎖モデルに関する最近の研究（Nguyen, Poli, et al. 2023）と同じ設定で、MambaをプリトレーニングとファインチューニングのためのFMバックボーンとして調査する。特に、モデルサイズと配列長に渡るスケーリング則の2つの探索（図5）と、長い文脈を必要とする難しい下流の合成分類タスク（図6）に焦点を当てる。

事前学習では、学習とモデルの詳細について、標準的な因果言語モデリング（次のトークン予測）のセットアップにほぼ従う（付録E.2も参照）。データセットについては、HyenaDNA（Nguyen, Poli, et al. 2023）のセットアップをほぼ踏襲している。HyenaDNAは、約45億のトークン（DNA塩基対）を持つ単一のヒトゲノムで構成されるHG38データセットを事前学習に用いている。

4.3.1 Scaling: Model Size

この実験では、様々なモデルのバックボーンを用いて、ゲノミクス基盤モデルのスケーリング特性を調べる（図5左）。

訓練。セクション4.3.2で示したように、配列長が長くなるとMambaがより有利になることが予想される。グローバルバッチサイズを1024に固定し、1バッチあたり $2^{20} \approx 1M$ トークンを学習する。モデルは $10K$ の勾配ステップで学習され、合計 $10B$ のトークンが学習された。

結果。図5(左)は、Mambaの事前学習の複雑さがモデルサイズとともに滑らかに向上すること、そしてMambaがHyenaDNAとTransformer++の両方よりも優れたスケールを持つことを示している。例えば、最大のモデルサイズである $\approx 40M$ パラメータでは、MambaはTransformer++とHyenaDNAのモデルにおよそ3倍から4倍少ないパラメータで匹敵することを示している。

4.3.2 Scaling: Context Length

次のDNA実験では、配列長に対するモデルのスケーリング特性を調べる。配列長が長くなると2次アテンションは法外に高価になるため、HyenaDNAとMambaモデルのみを比較する。配列長 $2^{10}=1024$ 、 $2^{12}=4096$ 、 $2^{14}=16384$ 、 $2^{16}=65536$ 、 $2^{18}=262144$ 、 $2^{20}=1048576$ でモデルを事前訓練する。モデルサイズは6層×幅128（約1.3M-1.4Mパラメータ）とした。モデルは $20K$ 勾配ステップで合計 $\approx 330B$ トークンで学習された。配列長が長い場合は、(Nguyen, Poli, et al. 2023)と同様の配列長ウォームアップを用いた。

結果図5（右）は、Mambaが長さ1Mの非常に長い配列まで、より長い文脈を利用することができ、文脈が増えるにつれて事前学習のperplexityが向上することを示している。一方、HyenaDNAモデルは配列の長さとともに悪化する。これはセクション3.5の選択メカニズムの特性に関する議論から直感的に理解できる。特に、LTIモデルは情報を選択的に無視することはできない。畳み込みの観点から見ると、非常に長い畳み込みカーネルは、非常にノイズが多い可能性のある長いシーケンス全体のすべての情報を集約することになる。HyenaDNAは文脈が長いほど改善すると主張しているが、その結果は計算時間を制御していないことに注意されたい。

4.3.3 Synthetic Species Classification

DNAの連続するセグメントをランダムにサンプリングして5つの異なる種を分類するという下流のタスクでモデルを評価する。このタスクは、｛ヒト、キツネザル、マウス、ブタ、カバ｝の種を用いたHyenaDNAから採用した。我々は、DNAの99％を共有することが知られている5種の類人猿｛ヒト、チンパンジー、ゴリラ、オランウータン、ボノボ｝の間を分類することで、かなり難易度の高いタスクに変更した。

4.4 Audio Modeling and Generation

音声波形モダリティについては、主にSaShiMiアーキテクチャと学習プロトコル（Goel et al. 2022）を比較する。このモデルは、

U-Netバックボーンと、各ステージごとにモデル次元 $D$ を2倍にする係数 $p$ による2段階のプーリング
各ステージにおけるS4ブロックとMLPブロックの交互配置

から構成される。

S4+MLP ブロックを Mamba ブロックに置き換えることを検討した。実験の詳細は付録 E.4 を参照。

4.4.1 Long-Context Autoregressive Pretraining

YouTubeMix（DeepSound 2017）で事前学習品質（自己回帰次サンプル予測）を評価する。YouTubeMixは、16000Hzのレートでサンプリングされた4時間のピアノ独奏曲からなる、先行研究で使用された標準的なピアノ音楽データセットである。事前学習の詳細は、ほぼ標準的な言語モデリングのセットアップ（セクション4.2）に従う。図7は、学習シーケンスの長さを $2^{13}=8192$ から $2^{20} \approx 10^6$ まで増加させた場合の効果を評価したものである。（データの扱い方に若干のエッジケースがあるため、スケーリング曲線にねじれが生じる可能性がある。例えば、分単位のクリップしか利用できなかったため、最大配列長は $60s \cdot 16000Hz = 960000$ で結ばれている）。

MambaとSaShiMi(S4+MLP)のベースラインは、コンテキストの長さが長くなるにつれて一貫して改善する。主な指標はバイトあたりのビット数（BPB）であり、これは他のモダリティを事前学習するための標準的な負の対数尤度（NLL）損失の一定係数log(2)である。

この論文で、実数パラメータ化から複素数パラメータ化（セクション3.6）に切り替えたのはこの実験だけである。付録E.4で追加のアブレーションを示す。

4.4.2 Autoregressive Speech Generation

SC09はベンチマーク音声生成データセット（Donahue, McAuley, and Puckette 2019; Warden 2018）であり、16000Hzでサンプリングされた「0」から「9」までの数字の1秒クリップで構成され、非常に可変的な特性を持つ。我々はGoelら（2022）の自己回帰学習セットアップと生成プロトコルにほぼ従っている。

表4は、Goelら（2022）の様々なベースラインと比較したMamba-UNetモデルの自動化指標を示している。比較対象は、WaveNet (Oord et al. 2016)、SampleRNN (Mehri et al. 2017)、WaveGAN (Donahue, McAuley, and Puckette 2019)、DiffWave (Z. Kong et al. 2021)、SaShiMiである。小さなMambaモデルは、最先端の（そしてはるかに大きな）GANと拡散ベースのモデルを凌駕する。ベースラインにパラメータを合わせたより大きなモデルは、忠実度メトリクスをさらに劇的に改善する。

表5は、小さなMambaモデルを用いて、外側のステージと中央のステージの異なるアーキテクチャの組み合わせを調べたものである。外側のブロックではMambaがS4+MLPよりも一貫して優れており、中央のブロックではMamba > S4+MLP > MHA+MLPであることがわかる。

4.5 Speed and Memory Benchmarks

図8では、SSMスキャン操作（状態拡張 $N=16$ ）の速度と、Mambaのエンドツーエンドの推論スループットをベンチマークしている。我々の効率的なSSMスキャンは、シーケンス長2Kを超えると、我々の知る限り最高のアテンション実装（FlashAttention-2（Dao 2023））よりも高速であり、PyTorchの標準的なスキャン実装よりも最大20-40倍高速である。Mambaは、KVキャッシュがないため、同じようなサイズのTransformerよりも4-5倍高い推論スループットを達成している。例えば、Mamba-6.9B（未訓練）は、5倍小さいTransformer-1.3Bよりも高い推論スループットを持つ。詳細は付録E.5を参照のこと。付録E.5にはメモリ消費量のベンチマークも含まれている。

4.6 Model Ablations

チンチラのトークン数（図4と同じ設定）で、サイズ $\approx 350M$ のモデルで言語モデリングの設定に焦点を当てて、私たちのモデルのコンポーネントの一連の詳細な切除を実行する。

4.6.1 Architecture

表6は、アーキテクチャ（ブロック）とその内側のSSM層（図3）の効果を調べたものである。

我々は、以下のことを発見した。

これまでの非選択的（LTI）SSMのうち、グローバル畳み込みに相当するものでは、性能は非常によく似ている。
このことは、ハードウェア効率を考慮すると、（少なくともLMでは）実数値SSMの方が良い選択であることを示唆している。
これらのいずれかを選択的SSM（S6）に置き換えると性能が大幅に向上し、セクション3の動機が検証される。
Mambaアーキテクチャの性能はH3アーキテクチャとほぼ同じである（選択レイヤーを使用した場合は若干良いようである）。

付録E.2.2では、MambaブロックとMLP（伝統的なアーキテクチャー）MHA（ハイブリッドアテンションアーキテクチャー）などの他のブロックとのインターリーブも調査している。

4.6.2 Selective SSM

表7は、選択的な $\Delta, B, C$ パラメータ（アルゴリズム2）の異なる組み合わせを考慮することにより、選択的なSSM層を切除し、RNNゲーティング（定理1）との関係により、 $\Delta$ が最も重要なパラメータであることを示している。

表8は、SSMの異なる初期化を考慮したもので、いくつかのデータモダリティや設定において大きな違いがあることが示されている（Gu, Goel, and Ré 2022; Gu, Gupta, et al. 2022）。言語モデリングでは、より標準的な複素数値のパラメータ化（S4D-Lin、1行目）ではなく、より単純な実数値の対角初期化（S4D-Real、3行目）の方が良い結果が得られる。ランダムな初期化もうまくいき、先行研究(Mehta et al. 2023)の結果と一致する。

表9と表10は、それぞれ $\Delta$ と $(B, C)$ プロジェクションの次元を変えることを検討している。静的な投影から選択的な投影に変更することで、最も大きな効果が得られるが、次元をさらに増やすと、一般的に、パラメータ数が少し増えるだけで、性能がわずかに向上する。

特に注目すべきは、状態サイズ $N$ を大きくしたときの選択的SSMの劇的な改善であり、わずか1％の追加パラメータのコストで1.0以上のperplexsityの改善が見られる。これは3.1節と3.3節で述べた我々の動機の核心を検証するものである。

5. Discussion

関連する仕事、限界、将来の方向性について述べる。

関連研究。付録Aは、選択メカニズムが類似の概念とどのように関連しているかを論じる。付録Bは、SSMと他の関連モデルの拡張された関連作業である。

ノーフリーランチ：連続-離散スペクトル。　構造化SSMはもともと連続システムの離散化として定義され(1)、知覚信号（例：オーディオ、ビデオ）のような連続時間データモダリティに強い帰納的バイアスを持つ。セクション3.1と3.5で議論したように、選択メカニズムはテキストやDNAのような離散モダリティでの弱点を克服しているが、これは逆にLTI SSMが得意とするデータでの性能を阻害する可能性がある。音声波形に関する我々のアブレーションでは、このトレードオフをより詳細に検証している。

ダウンストリーム・アフォーダンス Transformerベースの基盤モデル（特にLLM）には、微調整、適応、プロンプト、コンテキスト内学習、命令チューニング、RLHF、量子化など、事前学習されたモデルとの相互作用の特性や態様の豊かな生態系がある。私たちは、SSMのようなTransformerの代替手段が同様の特性やアフォーダンスを持っているかどうかに特に興味がある。

スケーリング。我々の実証的な評価は小さなモデルサイズに限定されており、ほとんどの強力なオープンソースLLM（例えばLlama（Touvron et al. 1023））や、RWKV（B. Peng et al. 2023）、RetNet（Y. Sun et al. 2023）などの他のリカレントモデルと同様に、7Bパラメータスケール以上で評価されている。Mambaがこのような大きなサイズでも有利に比較できるかどうかを評価する必要がある。また、SSMのスケーリングには、本論文では議論していない更なる工学的な課題やモデルの調整が含まれる可能性があることに注意する。

6. Conclusion

我々は構造化状態空間モデルに選択メカニズムを導入し、シーケンスの長さを線形にスケーリングしながら、コンテキスト依存の推論を行うことを可能にする。単純なアテンションフリーアーキテクチャに組み込むことで、Mambaは多様なドメインにおいて最先端の結果を達成し、強力なTransformerモデルの性能に匹敵するか、それを上回る。我々は、選択的状態空間モデルが、様々なドメイン、特にゲノム、オーディオ、ビデオなどの長い文脈を必要とする新しいモダリティのための基礎モデルを構築するための幅広い応用に期待している。我々の結果は、Mambaが一般的な配列モデルのバックボーンとなる有力な候補であることを示唆している。

2023-11-21

Understanding RetNet①: Theory of Retention

In a paper of RetNet, regarded as a successor to Transformer, particularly in Chapter Two, the architecture of RetNet is explained.

However, the formula in the paper is a little confusing. In this post, the details of formula is explained while filling in the gaps.

arxiv.org

*This is based on my understanding, so please comment if something seems incorrect.

Retentive Network

RetNet, similar to Transformer, is structured with a stack of $L$ identical blocks. Each block contains a Multi-Scale Retention and Feed Forward Network module, with RMS Norm and Residual Connection performed before and after these modules. Essentially, each block of RetNet is akin to a Transformer block, but with RMS Norm replacing Layer Norm, Multi-Scale Retention substituted by Multi-head Attention, and also performs relative position embedding, hence not requiring absolute position embedding. (Please refer to the paper for more detailed information.)

RetNet computes contextually embedded vectors $X^l = \text{RetNet}_l ( X^{l-1} ) , l \in [1, L$ ] when input vectors ${ \textbf{x} }_{i=1}^{|x|}$ are embedded into $X^0 = [ \textbf{x}_1, \cdots, \textbf{x}_{|x|} ] \in \mathbb{R}^{|x| \times d_{model} }$ .

Retention

The Retention mechanism has two forms: recursive and parallel, allowing for parallel training while making recursive inferences.

Given $X \in \mathbb{R}^{|x| \times d_{model} }$ , a trainable matrix $W_V \in \mathbb{R}^{d \times d}$ is used to compute $V = X W_V$ . For a token $X_n$ at time $n$ , the value $V_n = X_n \cdot w_V$ (the $n$ th row of $V$ ) and the state at the previous time $n-1$ , $s_{n-1}$ , are used to model a mapping $v(n) \mapsto o(n)$ that computes the $n$ th token of the transformed sequence.

In RetNet, this mapping is represented recursively as follows:

$\displaystyle \begin{align} s_n &= A s_{n-1} + K_n^T V_n　\quad &A \in \mathbb{R}^{d \times d}, K_n \in \mathbb{R}^{1 \times d} \\ o_n &= Q_n s_n = \sum_{m=1}^{n} Q_n A^{n-m} K^T_m V_m &Q_n \in \mathbb{R}^{1 \times d} \tag{1} \end{align}$

Here, query and key, like value, are determined using trainable matrices $W_Q, W_K \in \mathbb{R}^{d \times d}$ , with follows. $Q = X W_Q, K = X W_K \tag{2}$

$Q_n, K_n \in \mathbb{R}^{1 \times d}$ are respectively the $n$ th row vectors of $Q, K \in \mathbb{R}^{|x| \times d_{model} }$ , corresponding to the query and key for token $X_n$ .

The second equation of (1) may be less intuitive. To understand it, let's sequentially compute $s_1, s_2, s_3$ from the first equation:

$\displaystyle \begin{align} s_1 &= A s_0 + K_1^T v_1 \\ s_2 &= A s_1 + K_2^T v_2 = A (A s_0 + K_1^T v_1) + K_2^T v_2 = A^2 s_0 + A K_1^T v_1 + K_2^T v_2 \\ s_3 &= A s_2 + K_3^T v_3 = A (A^2 s_0 + A K_1^T v_1 + K_2^T v_2 ) + K_3^T v_3 \\ &= A^3 s_0 + ( A^2 K_1^T v_1 + A K_2^T v_2 + K_3^T v_3 ) = A^3 s_0 + \sum_{m=1}^{3} A^{3-m} K^T_m V_m \end{align}$

From here, the general formula for $s_n$ can be derived from the first recursive formula:

$\displaystyle s_n = A s_{n-1} + K_n^T V_n = A^n s_0 + \sum_{m=1}^{n} A^{n-m} K^T_m V_m$

Setting $s_0 = 0$ , we derive $o_n = Q_n s_n = \sum_{m=1}^{n} Q_n A^{n-m} K^T_m V_m$ .

Next, the square matrix $A$ is assumed to be diagonalizable with a regular matrix $\Lambda$ and $\gamma, \theta \in \mathbb{R}^d$ , such that $\Lambda^{-1} A \Lambda = \gamma e^{i \theta}$ . For those who want to review diagonalization, see wiki. Here, although $\theta \in \mathbb{R}^d$ , $\gamma e^{i \theta} \in \mathbb{R}^{d \times d}$ is represented as follows. This topic is also discussed in github's issue.

$\displaystyle \begin{align} ( \gamma e^{i \theta} ) = \begin{pmatrix} \gamma_1 e^{i \theta_1} & 0 & \cdots & 0 \\ 0 & \gamma_2 e^{i \theta_2} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \gamma_d e^{i \theta_d} \end{pmatrix} \end{align}$

Consequently, $A = \Lambda ( \gamma e^{i \theta} ) \Lambda^{-1}$ , and $A^{n-m}$ can be computed as:

$\displaystyle \begin{align} A^{n-m} &= ( \Lambda ( \gamma e^{i \theta} ) \Lambda^{-1} ) ( \Lambda ( \gamma e^{i \theta} ) \Lambda^{-1} ) \cdots ( \Lambda ( \gamma e^{i \theta} ) \Lambda^{-1} ) \\ &= \Lambda ( \gamma e^{i \theta} ) ( \Lambda^{-1} \Lambda ) ( \gamma e^{i \theta} ) ( \Lambda^{-1} \cdots \Lambda ) ( \gamma e^{i \theta} ) \Lambda^{-1} \\ &= \Lambda ( \gamma e^{i \theta} )^{n-m} \Lambda^{-1} \end{align}$

Thus, the second equation of (1) can be expressed as:

$\displaystyle \begin{align} o_n &= \sum_{m=1}^{n} Q_n \Lambda \left( \gamma e^{i \theta} \right)^{n-m} \Lambda^{-1} K^T_m V_m = \sum_{m=1}^{n} (X_n w_Q) \Lambda \left( \gamma e^{i \theta} \right)^{n-m} \Lambda^{-1} (w_K^T X_m^T) V_m \\ &= \sum_{m=1}^{n} X_n (w_Q \Lambda) \left( \gamma e^{i \theta} \right)^{n-m} (w_K (\Lambda^{-1})^T )^T X_m^T V_m \end{align}$

In the formula, $\Lambda$ is multiplied by the trainable parameters $w_Q, w_K$ , so instead of being separate parameters, they are absorbed into $w_Q, w_K$ and learned together.

Therefore, it is represented as:

$\displaystyle \begin{align} o_n &= \sum_{m=1}^{n} Q_n \left( \gamma e^{i \theta} \right)^{n-m} K_m^T V_m \\ &= \sum_{m=1}^{n} Q_n \left( \gamma e^{i n \theta} \right) \left( \gamma e^{- i m \theta} \right) K_m^T V_m \\ &= \sum_{m=1}^{n} (Q_n \left( \gamma e^{i n \theta} \right) ) \left( \gamma e^{-i m \theta} \right)^T K_m^T V_m \\ &= \sum_{m=1}^{n} (Q_n \left( \gamma e^{i n \theta} \right) ) \left( K_m (\gamma e^{ -i m \theta} ) \right)^T V_m \end{align}$

Here, $( \gamma e^{i \theta} )$ being a diagonal matrix, $( \gamma e^{i \theta} ) = ( \gamma e^{i \theta} )^T$ is used. $Q_n ( \gamma e^{i n \theta} )$ , $K_m ( \gamma e^{- i m \theta} )$ are known as xPos embeddings. (Interestingly, the authors of xPos and RetNet are almost the same. It seems the team from Seika University that developed xPos was recruited by Microsoft Research.)

For further simplification, treating $\gamma$ as a scalar leads to:

$\displaystyle o_n = \sum_{m=1}^{n} \gamma^{n-m} (Q_n e^{in \theta}) ( K_m e^{im \theta} )^{\dagger} V_m \tag{3}$

The definition of $e^{i n \theta}$ is as follows:

$\displaystyle e^{i n \theta} = \begin{pmatrix} e^{i n \theta_1} & 0 & \cdots & 0 \\ 0 & e^{i n \theta_2} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots &e^{i n \theta_d} \end{pmatrix}$

In this definition, although $\theta \in \mathbb{R}$ , $e^{i n \theta} \in \mathbb{R}^{d \times d}$ can be confusing. Therefore, redefining

and setting $Q_n = [ q_1, \ldots, q_d$ ], $Q_n e^{i n \theta}$ can be expressed as:

Hence, $o_n$ can be represented as:

$\displaystyle o_n = \sum_{m=1}^{n} \gamma^{n-m} (Q_n \odot e^{in \theta}) ( K_m \odot e^{im \theta} )^{\dagger} V_m \tag{4}$

Parallel Representation

Furthermore, defining $\Theta \in \mathbb{R}^{|x| \times d_{model}}$ as a compilation of $e^{i n \theta}$ for all time steps:

$\displaystyle \Theta = \begin{pmatrix} e^{i \theta} \\ \vdots \\ e^{i |x| \theta} \end{pmatrix}$

Then, redefining $Q, K \in \mathbb{R}^{|x| \times d_{model}}$ to include $Q_n \odot e^{i n \theta}$ and $K_n \odot e^{- i n \theta}$ for each time step respectively, they become:

$\displaystyle Q = \begin{pmatrix} Q_1 \odot e^{i \theta} \\ \vdots \\ Q_{|x|} \odot e^{i |x| \theta} \end{pmatrix} = \begin{pmatrix} Q_1 \\ \vdots \\ Q_{|x|} \end{pmatrix} \odot \Theta \\ = (X W_Q) \odot \Theta$

$\displaystyle K = \begin{pmatrix} K_1 \odot e^{- i \theta} \\ \vdots \\ K_{|x|} \odot e^{- i |x| \theta} \end{pmatrix} = \begin{pmatrix} K_1 \\ \vdots \\ K_{|x|} \end{pmatrix} \odot \bar{\Theta} \\ = (X W_K) \odot \bar{\Theta}$

The transformed vector for the entire input sequence $X$ , $\text{Retention} (X)$ , is expressed with $Q_n^{\prime} = Q_n \odot e^{in \theta}, K_m^{\prime} = K_m \odot e^{im \theta}$ as follows:

$\displaystyle \text{Retention} (X) = \begin{pmatrix} o_1 \\ \vdots \\ o_|x| \end{pmatrix} \\ = \begin{pmatrix} \sum_{m=1}^{1} \gamma^{1-m} Q_1^{\prime} K_m^{\prime \dagger} V_m \\ \vdots \\ \sum_{m=1}^{|x|} \gamma^{|x|-m} Q_{|x|}^{\prime} K_m^{\prime \dagger} V_m \end{pmatrix}$

$\displaystyle = \left( \begin{pmatrix} Q_1^{\prime} K_1^{\prime \dagger}, \ldots, Q_1^{\prime} K_{|x|}^{\prime \dagger} \\ \vdots \\ Q_{|x|}^{\prime} K_1^{\prime \dagger}, \ldots, Q_{|x|}^{\prime} K_{|x|}^{\prime \dagger} \end{pmatrix} \odot \begin{pmatrix} \gamma^{1-1}, 0, 0, \ldots, 0 \\ \gamma^{2-1}, \gamma^{2-2}, 0, \ldots, 0 \\ \vdots \\ \gamma^{|x|-1}, \ldots, \gamma^{|x|-|x|} \end{pmatrix} \right) \begin{pmatrix} V_1 \\ \vdots \\ V_{|x|} \end{pmatrix} \\$

$\displaystyle = (QK^T \odot D) V \tag{5}$

ここで、

$\displaystyle D_{nm} = \left\{ \begin{array}{ll} \gamma^{n-m} & (n \geq m)\\ 0 & (n < m) \end{array} \right.$

This form (5) represents Retention in parallel and is used for calculations during training.

Recurrent Representation

Expressing equation (4) using $Q_n^{\prime}, K_m^{\prime}$ results in:

$\displaystyle o_n = \sum_{m=1}^{n} \gamma^{n-m} Q_n^{\prime} K_m^{\prime \dagger} V_m$

Comparing this with equation (1), it becomes clear that the following holds:

$\displaystyle \begin{align} s_n &= \gamma s_{n-1} + K_n^{\prime T} V_n　\\ \text{Retention} (X_n) &= Q_n^{\prime} s_n = \sum_{m=1}^{n} Q_n^{\prime} {\gamma}^{n-m} K^{\prime T}_m V_m, \quad n = 1, \ldots, |x| \tag{6} \end{align}$

This is the recurrent form of RetNet, and during inference, the next token is predicted recursively using this formula.

Attention vs Retention

Attention is represented as:

$\displaystyle \text{Attention} (X) = \text{softmax}(QK^T \odot M ) V \tag{7}$

Here, $M$ is an Attention mask, for simplicity, assumed to be a decoder mask represented as:

$\displaystyle (M)_{n,m} = \left\{ \begin{array}{ll} 1 & (n \geq m)\\ 0 & (n < m) \end{array} \right.$

Thus, $\text{softmax}(QK^T \odot M )$ can be expressed as:

$\displaystyle \text{softmax} (QK^T \odot M) = \begin{pmatrix} \frac{ exp ( Q_1 K_1^T ) }{ \sum_{m=1}^{1} exp ( Q_1 K_m^T ) } , 0, \ldots, 0, 0 \\ \frac{ exp ( Q_2 K_1^T ) }{ \sum_{m=1}^{2} exp ( Q_2 K_m^T ) } , \frac{ exp ( Q_2 K_2^T ) }{ \sum_{m=1}^{2} exp ( Q_2 K_m^T ) }, \ldots, 0 \\ \vdots \\ \frac{ exp ( Q_{|x|} K_1^T ) }{ \sum_{m=1}^{|x|} exp ( Q_{|x|} K_m^T ) } , \frac{ exp ( Q_{|x|} K_2^T ) }{ \sum_{m=1}^{|x|} exp ( Q_{|x|} K_m^T ) }, \ldots, \frac{ exp ( Q_{|x|} K_{|x|}^T ) }{ \sum_{m=1}^{|x|} exp ( Q_{|x|} K_m^T ) } \\ \end{pmatrix}$

Therefore,

$\displaystyle (\text{softmax} (QK^T \odot M) )_{n,m} = \left\{ \begin{array}{ll} \frac{ exp ( Q_{n} K_m^T ) }{ \sum_{m=1}^{n} exp ( Q_{n} K_m^T ) } & (n \geq m)\\ 0 & (n < m) \end{array} \right.$

Let's consider the output $o_n$ of $\text{Attention} (X)$ at a certain time $n$ .

$\displaystyle \text{Attention} (X) = \begin{pmatrix} o_1 \\ \vdots \\ o_{|x|} \\ \end{pmatrix} = \begin{pmatrix} \sum_{m=1}^{1} \frac{ exp ( Q_1 K_m^T ) }{ \sum_{m=1}^{1} exp ( Q_1 K_m^T ) } V_m \\ \vdots \\ \sum_{m=1}^{|x|} \frac{ exp ( Q_{|x|} K_m^T ) }{ \sum_{m=1}^{|x|} exp ( Q_{|x|} K_m^T ) } V_m \\ \end{pmatrix}$

Therefore, $o_n$ can be expressed as:

$\displaystyle o_n = \sum_{m=1}^{n} \frac{ exp ( Q_n K_m^T ) }{ \sum_{m=1}^{n} exp ( Q_n K_m^T ) } V_m \tag{8}$

In Attention, only the current $Q_n$ is needed to calculate the output at time $n$ , but all previous values of keys and values must be computed, resulting in a computational complexity of $O(n)$ for inference.

However, with Retention, as shown below, calculations using keys and values up to time $n-1$ can be separated and retained as state, allowing each time step to have a computational complexity of $O(1)$ .

$\displaystyle o_n = Q_n^{\prime} \sum_{m=1}^{n} \gamma^{n-m} K_m^{\prime \dagger} V_m = Q_n^{\prime} \left( \gamma \left( \sum_{m=1}^{n-1} \gamma^{n-1-m} K_m^{\prime \dagger} V_m \right) + K_n^{\prime \dagger} V_n \right) \\ = Q_n^{\prime} \left( \gamma s_{n-1} + K_n^{\prime \dagger} V_n \right)$

That concludes this section. Next time, I will write about the theory and implementation of the relative position embedding xPos.

2023-11-14

RetNetを完全に理解する①：Retentionメカニズム

Transformerの後継と称されるRetNetの以下の論文中にて、特に二章で解説されるRetNetのアーキテクチャについて、行間を埋めながら解説する。

arxiv.org

*自分の理解をもとに書いているので、違っているようでしたらコメントください。

Retentive Network

RetNetは、Transformerと同じように、 $L$ 個の同じブロックを積み重ねる形状をしており、それぞれのブロックが、Multi-Scale RetentionとFeed Forward Networkモジュールを持ち、それらの前後でそれぞれRMS NormとResidual Connectionが行われる。つまり、RetNetの各ブロックは、基本的にはTransformerブロックにおいて、Pre NormにしてLayer Normの代わりにRMS Normを行い、Multi-head AttentionをMulti-Scale Retentionで置き換えたもので、さらに相対位置埋め込みを行うので位置埋め込みを各層の入力前に行わないようなモデルである。（めっちゃざっくりと言ってるので細かいことは論文を読んでください。）

RetNetは、入力ベクトル $\{ \textbf{x}_i \}_{i=1}^{|x|}$ が単語埋め込みにより $X^0 = [ \textbf{x}_1, \cdots, \textbf{x}_{|x|} ] \in \mathbb{R}^{|x| \times d_{model} }$ に埋め込まれたとき、文脈づけられたベクトル $X^l = \text{RetNet}_l ( X^{l-1} ) , l \in [1, L ]$ を計算する。

Retention

Retentionメカニズムは、再帰形式と並列形式という二つの形式を持ち、並列に学習を行いながら、再帰的に推論を行うことが出来る。

入力 $X \in \mathbb{R}^{|x| \times d_{model} }$ が与えられたとき、学習可能な行列 $W_V \in \mathbb{R}^{d \times d}$ を用いて、 $V = X W_V$ を求める。時刻 $n$ におけるトークン $X_n$ から得られる時刻 $n$ におけるバリュー $V_n = X_n \cdot w_V$ （ $V$ の $n$ 行目のベクトル）と、一つ前の時刻 $n-1$ における状態 $s_{n-1}$ を使って、変換後の系列の $n$ 番目のトークン $o_n$ を求める写像 $v(n) \mapsto o(n)$ をモデリングする系列変換問題を考える。

RetNetでは、この写像は以下の再帰形式で表せる。

ここで、クエリーとキーは、バリューと同じように、学習可能な行列 $W_Q, W_K \in \mathbb{R}^{d \times d}$ を用いて、 $Q = X W_Q, K = X W_K \tag{2}$ で求められる。 $Q_n, K_n \in \mathbb{R}^{1 \times d}$ はそれぞれ $Q, K \in \mathbb{R}^{|x| \times d_{model} }$ の $n$ 行目のベクトルであり、それぞれトークン $X_n$ に対応するクエリとキーである。

式(1)で、二つ目の式がどうして出てきたのかが分かりづらい。

これを理解するためにまず、一つ目の式から以下のように $s_1, s_2, s_3$ を順次求めていく。

すると、実は一つ目の漸化式から $s_n$ の一般式が以下のように求められることが分かるだろう。

$\displaystyle s_n = A s_{n-1} + K_n^T V_n = A^n s_0 + \sum_{m=1}^{n} A^{n-m} K^T_m V_m$

この式において $s_0 = 0$ とすれば、 $o_n = Q_n s_n = \sum_{m=1}^{n} Q_n A^{n-m} K^T_m V_m$ が導かれる。

次に、正方行列 $A$ は、 $\Lambda$ を正則行列とし、 $\gamma, \theta \in \mathbb{R}^d$ として $\Lambda^{-1} A \Lambda = \gamma e^{i \theta}$ と対角化することが出来るものとしている。対角化を復習したい場合はwikiなどを参照されたい。ここで、 $\theta \in \mathbb{R}^d$ としているが、 $\gamma e^{i \theta} \in \mathbb{R}^{d \times d}$ であり、以下のように表される。ここら辺についてはgithubのissueでも議論している。

すると、 $A = \Lambda ( \gamma e^{i \theta} ) \Lambda^{-1}$ と表され、 $A^{n-m}$ は、以下のように求められる。

すると、式(1)の二つ目の式は、以下のように表せる。

式中で、 $\Lambda$ は、 $w_Q \Lambda$ 、 $w_K (\Lambda^{-1})^T$ のような形で学習可能パラメータ $w_Q, w_K$ と掛けられるため、別のパラメータとせず $w_Q, w_K$ に吸収されまとめて学習されるとする。

すると、以下のように表される。

ここで、 $( \gamma e^{i \theta} )$ は対角行列より、 $( \gamma e^{i \theta} ) = ( \gamma e^{i \theta} )^T$ であることを用いた。 $Q_n ( \gamma e^{i n \theta} )$ 、 $K_m ( \gamma e^{- i m \theta} )$ はxPosとして知られている位置埋め込みである。（ちなみにxPosの著者とRetNetの著者はほぼ同じ。xPosを開発した精華大学のチームがMicrosoft Researchに引き抜かれたようだ。）

さらに簡素化して $\gamma$ をスカラーとすることで、以下が導かれる。

$\displaystyle o_n = \sum_{m=1}^{n} \gamma^{n-m} (Q_n e^{in \theta}) ( K_m e^{im \theta} )^{\dagger} V_m \tag{3}$

ここで、 $e^{i n \theta}$ の定義は以下である。

この定義では、 $\theta \in \mathbb{R}$ であるのに、 $e^{i n \theta} \in \mathbb{R}^{d \times d}$ であるのでわかりづらい。ここで、 $e^{i n \theta} = [ e^{i n \theta_1} , \ldots, e^{i n \theta_d}$ ]と新たに定義し、 $Q_n = [ q_1, \ldots, q_d ]$ とすると、 $Q_n e^{i n \theta}$ は以下のように表せる。

$\displaystyle \begin{align} Q_n e^{i n \theta} &= [ q_1, \ldots, q_d ] \begin{pmatrix} e^{i n \theta_1} & 0 & \cdots & 0 \\ 0 & e^{i n \theta_2} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots &e^{i n \theta_d} \end{pmatrix} = [ q_1 e^{i n \theta_1} , \ldots, q_d e^{i n \theta_d} ] \\ &= Q_n \odot [ e^{i n \theta_1} , \ldots, e^{i n \theta_d} ] = Q_n \odot e^{i n \theta} \end{align}$

すると、 $o_n$ は以下のように表すことができる。

$\displaystyle o_n = \sum_{m=1}^{n} \gamma^{n-m} (Q_n \odot e^{in \theta}) ( K_m \odot e^{im \theta} )^{\dagger} V_m \tag{4}$

Parallel Representation

さらに、全時刻における $e^{i n \theta }$ をまとめて新たに $\Theta \in \mathbb{R}^{|x| \times d_{model} }$ を以下のように定義する。

$\displaystyle \Theta = \begin{pmatrix} e^{i \theta} \\ \vdots \\ e^{i |x| \theta} \end{pmatrix}$

そして、 $Q, K \in \mathbb{R}^{|x| \times d_{model} }$ を、各時刻における $Q_n \odot e^{i n \theta}$ および $K_n \odot e^{- i n \theta}$ をそれぞれ含むように定義し直すと、それぞれ以下のようになる。

さらに、入力系列 $X$ 全体を変換後のベクトルである $\text{Retention} (X)$ は、 $Q_n^{\prime} = Q_n \odot e^{in \theta}, K_m^{\prime} = K_m \odot e^{im \theta}$ とすると、以下のように表される。

$\displaystyle = (QK^T \odot D) V \tag{5}$

ここで、

$\displaystyle D_{nm} = \left\{ \begin{array}{ll} \gamma^{n-m} & (n \geq m)\\ 0 & (n < m) \end{array} \right.$

とした。

式(5)がRetentionの並列形式であり、学習時にはこの式に従って計算される。

Recurrent Representation

式(4)を $Q_n^{\prime}, K_m^{\prime}$ を用いて表すと、以下のようになる。

$\displaystyle o_n = \sum_{m=1}^{n} \gamma^{n-m} Q_n^{\prime} K_m^{\prime \dagger} V_m$

式(1)と見比べれば以下が成り立つのが分かるだろう。

これがRetNetの再帰形式であり、推論時はこの式によって再帰的に次トークンが予測される。

Attention vs Retention

Attentionは以下で表される。

$\displaystyle \text{Attention} (X) = \text{softmax}(QK^T \odot M ) V \tag{7}$

ここで、 $M$ はAttentionマスクであり、簡単のため、以下のように表されるデコーダマスクであるとする。

$\displaystyle (M)_{n,m} = \left\{ \begin{array}{ll} 1 & (n \geq m)\\ 0 & (n < m) \end{array} \right.$

すると、 $\text{softmax}(QK^T \odot M )$ は、以下のように表せる。

従って、

$\displaystyle (\text{softmax} (QK^T) \odot M )_{n,m} = \left\{ \begin{array}{ll} \frac{ exp ( Q_{n} K_m^T ) }{ \sum_{m=1}^{n} exp ( Q_{n} K_m^T ) } & (n \geq m)\\ 0 & (n < m) \end{array} \right.$

$\text{Attention} (X)$ のある時刻 $n$ における出力を $o_n$ とする。

従って、 $o_n$ は以下のように表せる。

$\displaystyle o_n = \sum_{m=1}^{n} \frac{ exp ( Q_n K_m^T ) }{ \sum_{m=1}^{n} exp ( Q_n K_m^T ) } V_m \tag{8}$

ここで、クエリはインデックス $n$ のみを持ち、時刻 $n$ の出力を計算するのに同時刻のクエリのみを必要とするのに対し、 $K, V$ はインデックス $m$ を持ち、時刻 $n$ での出力を計算するのにそれまでの全時刻のキー、バリューが必要になる。このため、キー、バリューは推論ごとにキャッシュされる。

Retentionの場合は、以下で表されるのであった。

$\displaystyle o_n = Q_n^{\prime} \sum_{m=1}^{n} \gamma^{n-m} K_m^{\prime \dagger} V_m$

$Retention(X) = (QK^T \odot D) V$ であり、 $Attention(X) = \text{Attention} (X) = \text{softmax}(QK^T \odot M ) V$ と一見して似た形をしているが、 $\text{softmax}$ を作用させているかどうかで、 $o_n$ が大きく異なっているのが見て取れるだろう。 Attentionでは、まず $O (n)$ で $(\text{softmax} (QK^T) \odot M )_{n,m} = \frac{ exp ( Q_n K_m^T ) }{ \sum_{m=1}^{n} exp ( Q_n K_m^T ) }$ を求めた後、さらに $O(n)$ で $o_n = \sum_{m=1}^{n} \frac{ exp ( Q_n K_m^T ) }{ \sum_{m=1}^{n} exp ( Q_n K_m^T ) } V_m$ を計算する。このようにクエリーは現時点での $Q_n$ を使えばよいが、これまでの値すべてのバリューとキーとそれぞれ計算を行う必要があるため、推論時の計算量は全体で $O(n)$ となってしまう。

しかしながら、Retentionでは、以下のように時刻 $n-1$ までのキーとバリューを用いる計算を分け、状態として保持することができ、各時刻での計算量は全体として $O(1)$ で済む。

以上。次はそのうち相対位置埋め込みxPosの理論と実装について書きます。

2023-06-21

今日の論文2023/06/20,21：ERNIE: Enhanced Language Representation with Informative Entities

今日の論文

ERNIE: Enhanced Language Representation with Informative Entities

aclanthology.org

License: Creative Commons Attribution 4.0 International License(CC-BY)

本記事は、原著の内容に基づき筆者が要約または翻訳したものです。以下の図は、そこから引用しています。

This article is my summary or translation based on the content of the original publication. The following figures are taken from it.

要点まとめ

大規模コーパスで事前学習されたBERTのようなニューラル言語表現モデルは、プレーンテキストから豊富な意味パターンをうまく捕捉し、様々なNLPタスクのパフォーマンスを一貫して向上させるためにファインチューンすることができます。しかし、既存の事前学習済み言語モデルは、より良い言語理解のために豊富な構造化知識事実を提供できる知識グラフ（KG）の組み込みをほとんど考慮していない。我々は、KGに含まれる情報量の多いエンティティが、外部知識を用いて言語表現を強化することができると主張する。本論文では、大規模なテキストコーパスとKGの両方を利用して、語彙、構文、知識情報を同時にフル活用できる拡張言語表現モデル（ERNIE）を学習する。実験結果は、ERNIEが様々な知識駆動型タスクで大幅な改善を達成し、一方で他の一般的なNLPタスクでは最先端モデルBERTと同等であることを実証している。コードとデータセットは今後公開される予定である。

github.com

1 序論

特徴ベース（Mikolov et al., 2013; Pennington et al., 2014; Peters et al., 2017, 2018）およびfファインチューニング（Dai and Le, 2015; Howard and Ruder, 2018; Radford et al., 2018; Devlin et al., 2019）アプローチを含む、事前に訓練した言語表現モデルは、テキストから豊富な言語情報を取得し、多くのNLPアプリケーションを支援できる。BERT（Devlin et al., 2019）は、最も最近提案されたモデルの1つとして、単純な微調整によって名前付きエンティティ再認識（Sang and De Meulder, 2003）、質問応答（Rajpurkar et al., 2016; Zellers et al., 2018）、自然言語推論（Bowman et al., 2015）、テキスト分類（Wang et al., 2018）を含む様々なNLPアプリケーションでSoTAの結果を得ている。

　事前学習済み言語表現モデルは有望な結果を達成し、多くのNLPタスクで通常の構成要素として働いているが、言語理解のための知識情報を組み込むことが軽視されている。図1に示すように、"Blowin' in the Wind”と"Chronicles: Volume One"について、それぞれ歌と本であることを知らなければ、エンティティタイピングタスクでBob Dylanの2つの職業、すなわち”songwriter"と"writer"を認識することは困難である。また、関係分類タスクでは、"composer"や"author"のような細かな関係を抽出することはほぼ不可能である。既存の学習済み言語表現モデルでは、この2つの文は"UNK wrote UNK in UNK"のように構文的にあいまいである。したがって、豊富な知識情報を考慮することで、より良い言語理解につながり、エンティティタイピングや関係分類など、様々な知識駆動型アプリケーションに利益をもたらす。

　言語表現モデルに外部知識を取り入れるには、主に2つの課題がある。（１）構造化知識のエンコーディング：与えられたテキストに関して、その関連する情報的事実をいかに効果的に抽出して言語表現モデルのKGにエンコードするかは重要な問題である。（２）異種情報の融合：言語表現の事前学習手順は知識表現手順と全く異なるため、二つの個別のベクトル空間が生じる。語彙、構文、知識の情報を融合させた特別な事前トレーニングの目的をどのように設計するかは、もう一つの課題である。

　上記の課題を克服するために、我々は、大規模なテキストコーパスとKGの両方で言語表現モデルを事前学習するERNIE（Enhanced Language RepresentatioN with Informative Entities）を提案する。

　（１）知識情報の抽出とエンコードのために、まずテキスト中で言及されている名前付きエンティティを認識し、これらの言及をKG中の対応するエンティティに整列する。KGのグラフベースの事実を直接利用する代わりに、TransE（Bordes et al., 2013）のような知識埋め込みアルゴリズムでKGのグラフ構造をエンコードし、情報エンティティ埋め込みをERNIEの入力とする。ERNIEは、テキストとKGの間の整列に基づき、知識モジュールのエンティティ表現を意味モジュールの基礎層に統合する。

　（２） BERTと同様に、事前学習目標として、マスク化言語モデルと次文予測を採用する。また、テキストと知識特徴のより良い融合のために、入力テキスト中の名前付きエンティティの整列をランダムにマスクし、モデルにKGから適切なエンティティを選択して整列を補完させるという新しい事前学習目的を設計した。既存の事前学習済み言語表現モデルは、局所的な文脈を利用してトークンを予測するだけであるが、我々の目的は、トークンとエンティティの両方を予測するために文脈と知識事実の両方を集約し、知識豊富な言語表現モデルを導くことをモデルに求める。

我々は、2つの知識駆動型NLPタスク、すなわち、エンティティタイピングと関係分類について実験を行った。実験の結果、ERNIEはこれらの知識駆動型タスクにおいて、語彙、構文、および知識情報を最大限に活用することで、SoTAモデルのBERTを大幅に上回る性能を発揮することがわかった。また、ERNIEを他の一般的なNLPタスクでも評価したところ、ERNIEは依然として同等の結果を得ることができた。

2 関連研究

テキストから言語情報を取得し、その情報を特定のNLPタスクに利用するために、言語表現モデルの事前学習に多くの努力が払われている。これらの事前学習アプローチは、特徴ベースアプローチとファインチューニングアプローチに分けられる。

　初期の研究（Collobert and Weston, 2008; Mikolov et al., 2013; Pennington et al, 2014）は、特徴ベースのアプローチを採用し、単語を分散表現に変換することに重点を置いている。これらの事前訓練された単語表現は、テキストのコーポラにおける統語的・意味的情報を捉えるため、様々なNLPモデルの入力埋め込みや初期化パラメータとして用いられることが多く、ランダム初期化パラメータよりも大きな改善をもたらす（Turian et al., 2014）。これらの単語レベルモデルは単語の多義性に悩まされることが多いため、Petersら（2018）はさらにシーケンスレベルモデル（ELMo）を採用し、異なる言語コンテキストにわたる複雑な単語の特徴を捉え、ELMoを使用してコンテキストを考慮した単語埋め込みを生成する。

　Dai and Le（2015）は、入力特徴として事前に訓練された言語表現を使用するだけの上記の特徴ベースの言語アプローチとは異なり、ラベル付けされていないテキストでオートエンコーダを訓練し、事前に訓練されたモデルアーキテクチャとパラメータを他の特定のNLPモデルの出発点として使用する。Dai and Le (2015)に触発され、ファインチューンのためのより多くの事前訓練された言語表現モデルが提案されている。Howard and Ruder（2018）は、ユニバーサル言語モデル（ULMFiT）を構築するためにAWD-LSTM（Merity et al., 2018）を提示する。Radfordら（2018）は、generative pre-trained Transformer (Vaswani et al., 2017) (GPT)を提案して、言語表現を学習している。Devlinら（2019）は、多層トランスフォーマーによる深層双方向モデル（BERT）を提案しており、様々なNLPタスクでSoTAの結果を達成している。

　特徴ベースとファインチューニングの両方の言語表現モデルが大きな成功を収めているものの、それらは知識情報の組み込みを無視している。最近の研究で実証されているように、余分な知識情報を注入すると、読解（Mihaylov and Frank,2018; Zhong et al., 2018）、機械翻訳（Zaremoodi et al.、2018）、自然言語推論（Chen et al.、2018）、知識獲得（Han et al.、2018a）、対話システム（Madotto et al.、2018）のようなタスクでオリジナルモデルを大幅に向上させることができる。したがって、我々は、余分な知識情報は、既存の事前学習モデルに効果的に利益をもたらすことができると主張する。実際、いくつかの研究では、外部KGを効果的に活用するために、単語とエンティティの表現学習を共同で行うことが試みられており、有望な結果を得ている（Wang et al., 2014; Toutanova et al., 2015; Han et al., 2016; Yamada et al., 2016; Cao et al., 2017, 2018）。Sunら（2019）は、知識による言語表現を強化するために、マスクド言語モデルの知識マスク戦略を提案している。本論文では、さらにコーポらとKGの両方を利用して、BERTに基づく拡張言語表現モデルを学習する。

3 手法

本節では、ERNIEの全体的なフレームワークとその詳細な実装を紹介する。モデルアーキテクチャは3.2節、情報主体の符号化と異種情報の融合を目的とした新規の事前学習タスクは3.4節、ファインチューンの詳細は3.5節である

3.1 記法

トークン列を $\{w_1, \ldots ,w_n \}$ 、 $n$ はトークン列の長さである、とする。一方、与えられたトークンに整列するエンティティ列を $\{e_1, \ldots, e_m \}$ とし、 $m$ はエンティティ列の長さであるとする。KGではすべてのトークンがエンティティに整列できるわけではないので、ほとんどの場合、 $m$ は $n$ と等しくないことに注意する。さらに、すべてのトークンを含む語彙全体を $\mathcal{V}$ 、KGのすべてのエンティティを含むエンティティリストを $\mathcal{E}$ とする。トークン $w \in \mathcal{V}$ に対応するエンティティ $e \in \mathcal{E}$ がある場合、それらの整列は $f(w)=e$ と定義される。本稿では、図2に示すように、エンティティをその名前付きエンティティフレーズの最初のトークンに整列する。

3.2 モデルアーキテクチャ

図2に示すように、ERNIEのモデル全体は2つのモジュールから構成されている。(1)入力トークンから基本的な語彙と構文情報を取得する下層のテキストエンコーダ（T-Encoder）、(2) 下層からのテキスト情報にトークン指向の余計な知識端情報を統合する上位知識型エンコーダ（K-Encoder）、これによりトークンとエンティティの異種情報を統合特徴空間に表現できるようにした。また、T-Encoderの層数をN、K-Encoderの層数をMと表記する。

具体的には、トークン列 $\{w_1, \ldots, w_n \}$ とそれに対応するエンティティ列 $\{e_1, \ldots,e_m \}$ が与えられたとき、テキストエンコーダはまず各トークンのトークン埋め込み、セグメント埋め込み、位置埋め込みを合計して入力埋め込みを計算し、次に語彙的、構文的特徴 $\{w_1,\ldots,w_n \}$ を以下のように計算する。

ここで、 $\text{T-Encoder}(\cdot)$ は、多層双方向トランスフォーマーエンコーダである。 $\text{T-Encoder}(\cdot)$ はBERTにおける実装と同一であり、BERTが普及しているため、このモジュールの包括的な説明は除外し、Devlinetら（2019）およびVaswani et al.（2017）を読者に紹介する。

$\{w_1,\ldots,w_n \}$ を計算した後、ERNIEは知識エンコーダK-Encoderを採用し、知識情報を言語表現に注入する。具体的には、効率的な知識埋め込みモデルTransE (Bordes et al., 2013)によって事前に訓練されたエンティティ埋め込み $\{e_1, \ldots,e_m \}$ で $\{e_1, \ldots,e_m \}$ を表現する。そして、 $\{w_1,\ldots,w_n \}$ と $\{e_1, \ldots,e_m \}$ の両方をK-Encoderに送り、異種情報を融合させ、最終出力埋め込みを計算する。

$\{w^o_1,\ldots,w^o_n \}$ と $\{e^o_1, \ldots,e^o_m \}$ は特定のタスクのための特徴として使用される。知識付きエンコーダK-Encoderの詳細については、3.3節で紹介する。

3.3 知識のあるエンコーダー

図2に示すように、知識エンコーダK-Encodercは、トークンとエンティティの両方を符号化し、それらの異種特徴を融合するために設計された積層アグリゲータで構成される。 $i$ 番目のアグリゲータでは、前のアグリゲータから入力されたトークン埋め込み $\{w^{(i-1}_1,\ldots,w^{(i-1)}_n \}$ とエンティティ埋め込み $\{e^{(i-1}_1,\ldots,e^{(i-1)}_n \}$ はそれぞれ二つのマルチヘッドセルフアテンション（MH-ATT）（Vaswani et al, 2017）に送り込まれる。

　そして、 $i$ 番目のアグリゲータは、トークンとエンティティの並びを相互に統合するための情報融合層を採用し、各トークンとエンティティの出力埋め込みを計算する。トークン $w_j$ とそれに並ぶエンティティ $e_k＝f(w_j)$ に対して、情報融合プロセスは以下の通りである、

ここで $h_j$ は、トークンとエンティティの両方の情報を統合した内側の隠れ状態である。 $\sigma(\cdot)$ は非線形活性化関数であり、通常はGELU関数（Hendrycks and Gimpel, 2016）である。対応するエンティティのないトークンについては、情報融合層は以下のように統合せずに出力エンベッディングを計算する、

簡単のため、 $i$ 番目のアグリゲータ演算を以下のように表記する、

トップアグリゲータが計算したトークンとエンティティの埋め込み出力は、知識エンコーダK-Encoderの最終出力埋め込みとして使用される。

3.4 知識注入のための事前学習

情報エンティティによる言語表現に知識を注入するために、ERNIEに新たな事前学習タスクを提案する。このタスクでは、トークン-エンティティのアライメントをランダムにマスクし、アライメントされたトークンに基づいて対応するエンティティのすべてを予測するようにシステムに要求する。このタスクはノイズ除去オートエンコーダ（Vincent et al., 2008）の訓練に似ているため、この手順をノイズ除去オートエンコーダ(dEA)と呼ぶ。ソフトマックス層では $\mathcal{E}$ のサイズが非常に大きいことを考慮し、KG内のすべてのエンティティの代わりに、与えられたエンティティシーケンスに基づいてエンティティを事前検出することだけをシステムに要求する。トークン列 $\{w_1, \ldots, w_n \}$ とそれに対応するエンティティ列 $\{e_1, \ldots, e_m \}$ が与えられたとき、整列されたトークン $w_i$ のエンティティ分布を次のように定義する（[tex: \text{linear}(\cdot)は線形層）。式(7)は、dEAのクロスエントロピー損失関数を計算するために使用される。

トークン-エンティティの整列に誤差があることを考慮し、dEAのために以下の操作を行う： (1) 時間の5%は、あるトークンとエンティティの整列に対して、エンティティを別のランダムなエンティティに置き換える。これは、トークンが間違ったエンティティに整列されているというエラーを修正するために我々のモデルを訓練することを目的としている。 (2) トークン-エンティティの整列を15%の時間でマスクする。これは、エンティティの整列システムが既存の整列をすべて抽出しないエラーを修正するためにモデルを学習することを目的とする。(3) 残りの時間では、トークン-エンティティの整列を変更しない。これは、より良い言語理解のために、エンティティ情報をトークン表現に統合するようにモデルを促すことを目的としている。

　BERTと同様に、ERNIEも事前学習タスクとしてタスク付き言語モデル（MLM）と次世代予測（NSP）を採用し、ERNIEがテキスト中のトークンから語彙と構文の情報を取得できるようにする。これらの事前学習タスクの詳細は、Devlin et al.(2019)に記載されている。総合的な事前トレーニングの損失は、dEA、MLM、NSPの損失の合計である。

3.5 特定のタスクのためのファインチューニング

図3に示すように、様々な一般的なNLPタスクに対して、ERNIEはBERTと同様のファインチューン手順を採用することができる。特別な[CLS]トークンに対応する最初のトークンの最終出力埋め込みを、特定のタスクの入力シーケンスの表現とすることができる。いくつかの知識駆動タスク（例えば、関係分類やエンティティタイピング）については、特別なファインチューン手順を設計する。

　関係分類については、タスクは、与えられたエンティティペアの関係ラベルをコンテキストに基づいて分類することをシステムに求める。 ERNIEを関係分類のためにファインチューンする最も簡単な方法は、与えられたエンティティの言及の最終出力埋め込みにプーリング層を適用し、分類のためにそれらの言及埋め込みを連結したもので与えられたエンティティのペアを表現することである。本論文では、入力トークン列に2つのマークトークンを追加することで、エンティティの言及を強調する別の方法を設計する。これらのマークトークンは、従来の関係分類モデル（Zeng et al., 2015）における位置埋め込みと同様の役割を果たす。次に、分類のために[CLS]トークン埋め込みも取り入れる。ヘッド・エンティティとテール・エンティティには、それぞれ異なるトークン[HD]と[TL]を設計することに注意。

エンティティタイピングのための特定のファインチューニング手順は、関係分類の単純化バージョンである。先行するタイピングモデルが文脈埋め込みとエンティティ言及埋め込みの両方をフル活用するように（Shimaoka et al., 2016; Yaghoobzadeh and Sch ̈utze, 2017; Xin et al., 2018）、我々は、言及マークトークン[ENT]を持つ修正入力シーケンスが、文脈情報とエンティティ言及情報の両方を注意深く組み合わせるようにERNIEを導くことができると主張する。

4 実験

本節では、ERNIEの事前学習の詳細と、知識駆動型タスクと一般的なNLPタスクを含む5つのNLPデータセットにおけるファインチューニングの結果を示す。

4.1 事前学習データセット

事前学習手順は、主に言語モデルの事前学習に関する既存の文献に準拠したものである。 ERNIEを一から学習させるのはコストがかかるため、Googleが公開したBERTのパラメータを採用し、トークンをエンコードするTransformerブロックを初期化する。事前学習はNSP、MLM、dEAからなるマルチタスクであるため、事前学習用コーパスとして英語版Wikipediaを用い、テキストをWikidataに整列する。事前学習のためにコーパスをフォーマット化した後、アノテーション付き入力は約4500Mのサブワードと140Mのエンティティを持ち、3エンティティ未満の文は破棄される。

ERNIEを事前学習する前に、Wikidataに対してTransEで学習した知識埋め込みをエンティティの入力埋め込みとして採用した。具体的には、5,040,986個のエンティティと24,267,796個のファクトトリプルを含むWikidataの一部をサンプリングする。エンティティの埋め込みは学習中に固定され、エンティティエンコーディングモジュールのパラメータはすべてランダムに初期化される。

4.2 パラメータ設定とトレーニングの詳細

本論文では、トークンエンベッディングとエンティティエンベッディングの隠れ次元をそれぞれ $H_w, H_e$ とし、セルフアテンションヘッドの数をそれぞれ $A_w, A_e$ とする。具体的には、 $N= 6, M= 6, H_w=768, H_e= 100, A_w=12, A_e= 4$ というモデル規模である。BERTBASEのパラメータ総量は約110Mであり、ERNIEの知識モジュールは言語モジュールよりもはるかに小さく、ランタイムパフォーマンスにほとんど影響を与えないことがわかる。また、ERNIEの事前学習は、注釈付きコーパスを用いて1エポックのみ行った。学習プロセスを高速化するため、最大系列長を512から256に短縮した。これは、セルフアテンションの計算が長さの二次関数になるためである。また、バッチ内のトークン数をBERTと同じにするため、バッチサイズを2倍の512とした。学習率を $5e^{-5}$ に設定した以外は、BERTで使用した事前学習ハイパーパラメータをほぼ踏襲している。ファインチューニングのため、バッチサイズ、学習率、学習エポック数を除き、ほとんどのハイパーパラメータは事前学習と同じである。バッチサイズ：32、学習率（Adam）： $5e^{-5}$ 、 $3e^{-5}$ 、 $2e^{-5}$ 、エポック数：3から10。

　また、遠距離教師付きデータセットであるFIGER（Ling et al., 2015）についてもERINEを評価した。深く積み重ねられたTransformerブロックの強力な表現能力から、小さなバッチサイズではモデルが学習データをオーバーフィットすることがわかった。したがって、オーバーフィットを避けるために大きなバッチサイズと少ない学習エポックを使用し、学習率の範囲を変更しない、すなわち、バッチサイズ2048、エポック数2,3とした。

　ほとんどのデータセットにはエンティティの注釈がないため、TAGME (Ferragina and Scaiella, 2010)を用いて文中のエンティティの言及を抽出し、それらをKGの対応するエンティティにリンクさせる。

4.3 エンティティタイピング

エンティティの言及とそのコンテキストが与えられた場合、エンティティタイピングでは、システムがエンティティの言及にそれぞれのセマンティックタイプをラベル付けする必要がある。このタスクの性能を評価するために、FIGER (Ling et al., 2015) とOpen Entity (Choi et al., 2018) の2つの確立されたデータセットでERNIEをファインチューンする。FIGERの訓練セットはdistant supervisionでラベル付けされ、そのテストセットは人手によりアノテートさえる。Open Entityは完全に手動でアノテーションされたデータセットである。これら2つのデータセットの統計は表1に示されている。我々は我々のモデルを以下のエンティティタイピングのベースラインモデルと比較する。

NFGEC：NFGECはShimaokaら(2016)が提案したハイブリッドモデルである。NFGECは、入力として、エンティティの言及、コンテキスト、および特別なハンドクラフトの特徴を組み合わせており、FIGERにおけるSoTAモデルである。本論文では、様々なニューラルモデルの一般的な言語表現能力の比較に焦点を当てているため、この作業ではハンドクラフト特徴を使用しない。

UFET：Open Entityについては、新しいハイブリッドモデルUFET（Choi et al., 2018）を加えて比較する。UFETはOpen Entityデータセットで提案されており、NFGECのエンティティの言及で分離された2つのBi-LSTMの代わりに、コンテキスト表現にBi-LSTMを使用する。

　NFGECとUFETに加えて、公平な比較のために、セクション3.5で紹介した同じ入力形式でBERTをファインチューンした結果も報告している。 NFGEC、BERT、ERNIEをFIGER上で比較し、評価基準としてstrict accuracy, loose macro、loose microのスコアを採用した。

　FIGERの結果は表2の通りである。この結果から、以下のことがわかる。：(1) BERTは、NFGECとマクロおよびミクロの評価基準で同等の結果を得た。しかし、BERTはNFGECのベストモデルよりも精度が低い。strict precisionは、事前予測が人間の注釈と一致するインスタンスの割合であるため、BERTの強力なフィッティング能力により、distant supervisionからの誤ったラベルがBERTによって学習されることを示している。(2) BERTと比較して、ERNIEはstrict accuracyを大幅に向上させた。これは、外部知識がERNIEを正則化してノイズの多いラベルの適合を回避し、その結果、エンティティタイピングに有利になることを示している。

　Open Entityの結果を表3に示す。この表から、以下のことがわかる。：(1) BERTとERNIEは、従来のエンティティタイピングモデルよりもはるかに高いrecallスコアを達成している。これは、事前学習言語モデルが、教師なし事前学習と手動注釈付き学習データの両方を十分に活用し、より優れたエンティティタイピングを実現していることを意味している。(2) BERTと比較して、ERNIEはprecisionを2%向上させ、recallを2%向上させた。これは、情報エンティティがERNIEのラベル予測をより正確にするのに役立つことを意味する。

　要約すると、KGからの情報を注入することにより、distant supervisionエンティティタイプデータセットであるFIGERにおけるノイズラベル課題を効果的に軽減した。さらに、ERNIEは、ゴールドアノテーションを持つOpen Entityにおいてもベースラインを上回った。

4.4 関係分類

関係分類は、与えられたセンテンスにおける2つのエンティティ間の正確な関係を決定することを目的としており、これは重要な知識駆動型NLPタスクである。このタスクの性能を評価するために、2つの確立されたデータセットFewRel（Han et al, 2018c）とTACRED（Chang et al, 2017）でERNIEをファインチューンしている。2つのデータセットの統計は、表4に示すとおりである。FewRelの元々の実験設定はfew-shot学習であるため、FewRelデータセットを共通関係分類の設定に並べ替えた。具体的には、学習セットには各クラスから100インスタンス、開発セットとテストセットにはそれぞれ200インスタンスをサンプリングする。FewRelでは80クラス、TACREDでは42クラス（特殊関係「無関係」を含む）である。我々のモデルを、関係分類のための以下のベースライン・モデルと比較する。

CNN：畳み込み層、最大プール層、非線形活性化層からなるCNNは、出力文の埋め込みを取得し、それを関係分類器に供給する。先頭と末尾のエンティティの位置をより良く捉えるために、位置埋め込みがCNNに導入される（Zeng et al., 2015; Linet al., 2016; Wu et al., 2017; Han et al., 2018b）。

PA-LSTM：Zhangら（2017）は、LSTMネットワーク上にposition-awareなアテンションメカニズムを導入したPA-LSTMを提案しており、最終的な文の表現に対して、これらの文の各単語の相対寄与度を評価する。

C-GCN：Zhangら（2018）はグラフコンボリューション操作を採用して、関係分類の構文木をモデル化している。語順を符号化し、非順序解析におけるエラーの副作用を軽減するために、文脈化 GCN (C-GCN)は、まず、Bi-LSTM を用いて、文脈化された表現を GCN モデルの入力として生成する。

　これらの3つのベースラインに加え、公平な比較のために、セクション3.5で紹介した同じ入力フォーマットでBERTをファインチューンする。FewRel にはエンティティ間の関係がないnullインスタンスがないため、モデルの性能を示すためにマクロ平均のメトリクスを採用している。また、FewRelは文にWikidataのファクトが含まれているかどうかをチェックすることで構築されているため、公正な比較のために、事前学習前にKGの関連ファクトを削除している。表5から、2つの見解が得られる。 (1) CNNエンコーダを一から学習させるには、学習データが十分でないため、CNNのF1スコアは69.35%にとどまった。しかし、BERTとERNIEを含む事前学習モデルは、F1スコアを少なくとも15%向上させる。(2) ERNIEはBERTよりも絶対的に3.4%のF1増加を達成しており、外部知識の融合が非常に有効であることを意味している。

　TACREDでは、80%近いnullインスタンスがあるため、先行研究（Zhang et al., 2017）に従って、マクロではなくモデルのパーフォーマンスを表すマイクロ平均化メトリクスを採用している。CNN、PA-LSTM、C-GCNの結果は、Zhangら(2018)の論文に由来し、それぞれCNN、RNN、GCNの最高の結果である。表5から、我々は以下を観察する： (1) C-GCNモデルは、C-GCNが構文木とエンティティマスク戦略を利用し、0.4％のF1増加によって強いBERTモデルを上回る。エンティティマスク戦略とは、各サブジェクト（および同様にオブジェクト）エンティティを特殊NERトークンと置き換えることを指し、これは我々の提案する事前学習タスクdEAと同様である。 (2) ERNIEは、最高のrecallとF1スコアを達成し、BERTのF1を約2.0%向上させた。これは、知識モジュールが関係分類に有効であることを証明している。

　結論として、事前学習した言語モデルは、バニラエンコーダCNNとRNNよりも関係分類に多くの情報を提供できることがわかった。また、ERNIEは関係分類データセットの両方でBERTを上回ったが、特に学習セットがはるかに少ないFewRelでは上回った。これは、大規模な注釈付きデータが利用できない多くの自然言語処理タスクにとって重要なことである、小さな学習データを最大限に活用するために、余分な知識がモデルを助けることを示している。

4.5 GLUE

General Language Understanding Evaluation (GLUE)ベンチマーク（Wang et al., 2018）は、多様な自然言語理解タスクの集まりであり（Warstadt et al., 2018; Socher et al., 2013; Dolan and Brockett, 2005; Agirre et al., 2007; Williams et al., 2018; Rajpurkar et al., 2016; Dagan et al., 2006; Levesque et al., 2011）、Devlinら（2019）で使用された主要なベンチマークである。我々の知識改変が一般的なNLPタスクの性能を向上させるかどうかを調べるために、GLUEの8つのデータセットでERNIEを評価し、BERTと比較する。

　表6では、我々の評価投稿の結果とリーダーボードからのBERTの結果を報告している。 MNLI、QQP、QNLI、SST-2のような大きなデータセットでは、ERNIEはBERTBASEと一致していることが分かる。つまり、ERNIEはCoLAとRTEでは優れているが、STS-BとMRPCでは劣っている。

　要するに、ERNIEはGLUEでBERTBASEと同等の結果を達成している。一方では、GLUEが言語表現に外部知識を必要としないことを意味する。他方では、ERNIEは異種情報融合後にテキスト情報を失うことがないことを示す。

4.6 アブレーションスタディ

本節では、FewRelデータセットを用いたERNIEの事前学習タスク（dEA）と情報エンティティの効果を検証する。w/o enntitiesとw/o dEAは、それぞれ、エンティティ列入力のないERNIEと事前学習タスクdEAのファインチューニングを指す。表7に示すように、以下のことがわかった。(1) エンティティ列入力がない場合、dEAは事前学習で言語表現に知識情報を注入し、BERTのF1スコアを0.9%増加させる。 (2) 形成されたエンティティは、直感的に関係分類に役立つ多くの知識情報をもたらすが、dEAを用いないERNIEはこれをほとんど利用しないため、F1が0.7％増加した。

5 結論

本論文では、言語表現モデルに知識情報を取り入れるためのERNIEを提案する。本論文では、言語表現モデルに知識情報を組み込むためのERNIEを提案し、テキストと言語表現モデルの両方から得られる異質な情報をよりよく融合させるために、知識エッジ可能なアグリゲータと事前学習タスクdEAを提案する。実験結果は、ERNIEがBERTよりもdistant supervisionデータのノイズ除去や、限られたデータに対するファインチューニングに優れていることを示す。今後の研究には3つの重要な方向性が残されている：(1) ELMo（Peters et al., 2018）のような特徴ベースの事前学習モデルに知識を注入する。(2) 世界知識データベースWikidataとは異なるConceptNet (Speer and Havasi, 2012)などの言語表現モデルに多様な構造知識を導入する。(3) より大きな事前学習データの構築に向け、現実世界のコーポレーションを発見的に注釈付けする。このような方向性は、より一般的で効果的な言語理解につながる可能性がある。

2023-06-18

今日の論文2023/06/16,17：COMET: Commonsense Transformers for Automatic Knowledge Graph Construction

今日の論文

COMET: Commonsense Transformers for Automatic Knowledge Graph Construction

aclanthology.org

License: Creative Commons Attribution 4.0 International License(CC-BY)

本記事は、原著の内容に基づき筆者が要約または翻訳したものです。以下の図は、そこから引用しています。

This article is my summary or translation based on the content of the original publication. The following figures are taken from it.

要点まとめ

我々は、2つの普及しているコモンセンス知識グラフ、すなわち ATOMIC (Sap et al., 2019)とConceptNet (Speer et al., 2017)に対する自動知識ベース構築に関する最初の包括的な研究を発表する。正規のテンプレートで知識を格納する多くの従来のKBとは逆に、コモンセンスKBは知識の緩く構造化されたオープンテキスト記述のみを格納する。我々は、コモンセンスの自動補完に向けた重要なステップは、コモンセンス知識の生成モデルの開発であると仮定し、自然言語で豊かで多様なコモンセンス記述を生成することを学習するCOMmonsEnse Transformers (COMET)を提案する。コモンセンスモデリングの課題にもかかわらず、我々の調査では、事前に訓練された深い言語モデルからの暗黙知をコモンセンス知識グラフの明示的な知識を生成するために転送した場合、有望な結果が得られることが明らかにした。COMETは、人間が高品質と評価する新規知識を生成できることが実証され、トップ1では最大77.5%（ATOMIC）、91.7%（ConceptNet）の精度で、これらのリソースの人間のパフォーマンスに近づいた。この結果は、コモンセンスKBの自動補完に生成コモンセンスモデルを用いることが、抽出的な手法に代わる有力な選択肢となる可能性を示唆している。

1 序論

人間は文章を読むとき、提示された物語を理解するために、常識的な推論を行う。機械がこのような能力を獲得するためには、制限のない状況において、適切かつ正しい常識を獲得することができなければならない。この研究では、常識の獲得を知識ベース構築として捉え、大規模言語モデルが常識的な知識ベース（KB）を自動的に構築するために必要な知識を生成することを効果的に学習できるかどうかを調査する。

　自動KB構築は、高精度のキュレーションKBで高い概念網羅性を達成することが困難なため、人工知能研究の長年の目標である（Lenat, 1995; Miller, 1995）。これまでの研究では、半構造化テキスト(Suchanek et al., 2007; Hoffart et al., 2013; Aueret al., 2007; Bollacker et al., 2008) や非構造化テキスト (Dong et al., 2014; Carlson et al., 2010; Nakashole et al., 2011, 2012; Niu, 2012) を読み取り、ダウンストリームアプリケーションに照会できるリラショナルスキーマとして抽出できるモデルの開発が行われてきた。しかし、これらのアプローチに共通するのは、百科事典的な知識に焦点を当てることであり、これはモデル化できる実体と関係のよく定義された空間に適している。

　しかし、コモンセンスな知識は、2つのエンティティと既知の関係を比較するスキーマに明確に適合しないため、現在のアプローチは、「エンティティ」を自然言語のフレーズ、関係をそれらを結びつけることのできる任意の概念としてモデル化することになる（Li et al., 2016; Sap et al., 2019）。OpenIEのアプローチは、オープンテキストのエンティティと関係というこの特性を示すが（Etzioni et al., 2011; Fader et al.,2011; Mausam et al., 2012）、抽出的であるため、テキストで明示的に言及された知識しか捕捉できず、しばしば暗黙的である常識知識の取得に対する適用性が限られている（Gordon and Van Durme, 2013）。

　一方、深層文脈化言語モデルのトレーニングにおける最近の進歩（Peters et al.2018; Radford et al., 2018; Devlin et al., 2018）は、コモンセンスKB構築のための道として、外付けの方法を超えて探求する機会を提供します。これらの大規模言語モデルは、その基礎となる表現が最終的なタスクを解決するために調整されたときに素晴らしい性能を発揮し、さまざまな複雑な問題でSoTAの結果を達成している。この研究ではCOMMon sEnse Transformer(COMET)を定義し、既存のタプルを知識のシードセットとして使用することでコモンセンスKBを構築し、その知識を訓練する。このシードセットを用いて、事前に訓練された言語モデルは、学習された表現を知識生成に適応させることを学習し、高品質な新規タプルを生成する。

　この研究における我々の貢献を以下のように要約する。まず、知識ベース構築のための生成的アプローチを開発する。モデルは、既存のシードフレーズと関係タイプを首尾よく補完するフレーズを生成することによって、新しいノードを生成し、既存のノード間のエッジを識別するように学習する必要がある。次に、大規模な変換言語モデルを用いて、常識的な知識句を生成することを学習する枠組みを開発する。最後に、ATOMICとConceptNetの2つのドメインについて、本アプローチが生成する常識的な知識の質、新規性、多様性に関する実証研究と、効果的な知識モデルを学習するために必要なシードタプルの数に関する効率化研究を実施する。その結果、ATOMICイベントに対する生成タプルの77.5%、ConceptNetリラプションに対する生成タプルの91.7%が人間の判定によって正しいことが判明したことから、COMETは高品質のタプル生成に成功したことがわかった。

2 コモンセンスを生成するための学習

COMETは、知識タプルのシードセットに対して言語モデルを学習させることにより、言語モデルからコモンセンス知識ベースを構築する適応フレームワークである。これらのタプルは、学習すべき知識ベースの構造と関係をCOMETに提供し、COMETは、事前学習で学習した言語モデル表現を適応させて、新しいノードとエッジをシード知識グラフに追加することを学習する。

2.1 タスク

より具体的には、この問題はCOMETに $\{s, r, o \}$ 形式の自然言語タプルの学習知識ベースが与えられ、 $s$ がタプルのフレーズ主語、 $r$ がタプルの関係、 $o$ がタプルのフレーズ目的語であると仮定する。例えば、"taking a nap "に関連するConceptNetタプルは、次のようになる：s="take a nap", r=Causes, o="have energy"。タスクは与えられた $s$ と $r$ に対して $o$ を生成することである。

表記法： $X^s = \{ x^s_0, \ldots, x^s_{|s|} \}$ を関係の主語を構成するトークン、 $X^r = \{x^r_0, \ldots, x^r_{|r|} \}$ をタプルの関係を構成するトークン、 $X^o = \{x^o_0, \ldots, x^o_{|o|} \}$ をタプルのオブジェクトを構成するトークンとして定義する。任意の単語 $x$ に対する埋め込みを $e$ とする。

2.2 Transformer言語モデル

COMETは初期化される言語モデルに依存しないが、本研究では、Radfordら（2018）（GPT）で紹介されたTransformer言語モデルアーキテクチャを使用する。GPTは、マルチヘッドスケールドドットアテンションと完全連結層の複数のTransformerブロックを使用して入力テキストをエンコードする（Vaswani et al, 2017）。図2は、GPTアーキテクチャのさまざまなコンポーネントを示しており、以下、各コンポーネントをより深く定義している。

Transformer Block：図2(b)に示すように、各Transformerは、アーキテクチャ的に同一のTransformerブロック（ただし、ユニークなパラメータを持つ）を含み、そのブロックへの入力に以下の変換を適用する。

ここで、MULTIATTNはマルチヘッドのセルフアテンション機構（以下に定義）、FFNは2層のフィードフォワードネットワーク、LAYERNORMはセルフアテンションとフィードフォワードネットワークの出力に適用される層正規化（Ba et al., 2016）操作を表す。LAYERNORM操作の入力には、前の操作の出力と入力を合計した残差接続を含むことに注意すること。

マルチヘッドアテンション：図2(a)に示す各Transformerブロックのマルチヘッドアテンションモジュールは、Vaswaniら（2017）によって元々定義されたものと同じである。アテンション機能は、クエリQ、キーK、およびバリューVの3つの入力を受け取る。アテンションは、QとKを用いたVに対するユニークなスケールドットプロダクトアテンション分布を計算する複数のヘッドで構成されている：

ここで、 $d_k$ はクエリ、キー、バリューを表す入力ベクトルの次元数である。各ヘッドについて、Q、K、Vはアテンションが計算される前に一意的に投影される：

ここで、 $H_i$ は1つの注目ヘッドの出力、 $W^Q_i$ 、 $W^K_i$ 、 $W^V_i$ はそれぞれQ、K、Vに対するヘッド固有のプロジェクションである。そして、アテンションヘッド $H_i$ の出力は連結される：

ここで、 $W^O$ はアテンションヘッドの連結出力の出力投影である。図2(c)に示すように、我々はRadfordら（2018）に従い、前の層のトランスフォーマーブロックの出力を、次のブロックのマルチヘッドアテンションのクエリ入力として使用する。キーとバリューは、すべての先行する時間ステップの前のレイヤーのブロックの出力である：

ここで、 $h_{t}^{l-1}= \{ h^{l-1} \}_{\lt t}$ は、 $t$ 以前の時間ステップの前のトランスフォーマーブロック出力の集合である。

エンコーダ入力：モデルの入力として、知識タプル $\{s, r, o \}$ を、タプルの各項目の単語を連結したシーケンスとして表現しています：

Transformer（セルフアテンションモデル）にはトークンの順序の概念がないため、シーケンスの絶対位置ごとに位置埋め込み $p_t$ が初期化される（Vaswani et al, 2017）。任意の入力単語 $x_t \in X$ に対して、入力の我々のエンコーディングは、シーケンス $X$ 内の絶対位置をエンコードする位置エンベッディングと、その単語エンベッディング $e_t$ の合計である：

$h_t^0 = e_t + p_t$

ここで、 $p_t$ は時間ステップ $t$ の位置埋め込み、 $h_0$ は最初のトランスフォーマーレイヤーへの入力である。

3 COMETの学習

COMETは、知識タプルのフレーズサブジェクト $s$ と関係 $r$ が与えられたときに、そのフレーズオブジェクト $o$ を生成するように学習する。より具体的には、 $s$ と $r$ : $[ X_s, X_r$ ]のトークンの連結が入力として与えられた場合、モデルは $o X^o$ のトークンを生成するように学習しなければならない（これらの変数の定義については§2.1参照）。

損失関数：この目標を達成するために、COMETはフレーズオブジェクトのトークン $X^o$ を予測する条件付き対数尤度を最大化するように学習する：

ここで、 $|s|$ 、 $|r|$ 、 $|o|$ はそれぞれ主語句、関係句、目的語句のトークンの数である。図3は、異なる学習タスクのための $s$ 、 $r$ 、 $o$ 中のトークンがどのように構成されているかを概説している。

データセット：COMETは、既存のKBから知識エッジタプルのシードセットを使用して、コモンセンス知識の生成を学習する。この研究では、知識シードセットとしてATOMICとConceptNetを使っているが、COMETはドメインを問わず、他のコモンセンス知識再ソースも使用できた。

初期化：パラメタはRadfordら（2018）の最終言語モデル重みに初期化されている。微調整のために語彙に追加される特別なトークン（例えば、ATOMICのReactやConceptNetのISAなどの関係詞）は、標準正規分布からサンプリングして初期化する。

ハイパーパラメータ：Radfordら（2018）のGPTモデルの設計に従って、COMETに12層、768次元隠れ状態、12のアテンションヘッドを初期化する。ドロップアウト率は0.1、活性化関数としてGeLU（Hendrycks and Gimpel, 2016）ユニットを使用する。訓練中のバッチサイズは64である。その他のデータセット固有のハイパーパラメータは付録 A.1 に記載されている。

4 ATOMIC実験

Sapら（2019）が公開したATOMIC datasetは、特定のイベントプロンプト（例えば、「Xは店に行く」）周辺の様々な社会的コモンセンス知識をカバーする877Kタプルを含む。具体的には、ATOMICは、イベントの原因（例えば、「Xはそこに車で行く必要がある」）、エージェントへの影響（例えば、「食べ物を得る」）、他の直接（または暗示）参加者への影響（例えば、「他の人は食べ物を得る」）を網羅し、二次元でそのコモンセンスを蒸留しています。実験では、ATOMICイベント（例：「Xが店に行く」）はフレーズ主語、 $s$ 、次元（例：xIntent）はフレーズ関係、 $r$ 、原因／結果（例：「食べ物を得る」）はフレーズ対象、 $o$ とする。 Sapら（2019）のトレーニングスプリットを使用し、それぞれ710kトレーニング、80k開発、87kテストタプルになる。

4.1 セットアップ

指標：Sapら（2019）に従い、自動評価指標としてBLEU-2を用いて本手法を評価する。また、ゴールド応答におけるモデルのperplexityも報告する。表1の残りの自動評価指標は、トレーニングセットにない生成タプルと生成オブジェクトの比率を測定する。生成されたタプルのうち、新規のもの（% N/Tsro）と新規のオブジェクトを持つものの割合（% N/To）を報告する。これらの新規オブジェクトが多様であることを示すために（すなわち、同じ新規オブジェクトが唯一生成されるわけではない）、新規オブジェクトの数を、すべてのテストセットイベントに対して生成されたユニークなオブジェクトのセットの関数として報告します（% N/Uo）。

　最後に、Amazon Mechanical Turk (AMT)のワーカーを使った人間評価を行う。ワーカーは、ATOMIC commonsenseのモデル生成が、フレーズ主語、関係詞、フレーズ目的語のもっともらしいタプルを適切に補完しているかどうかを確認するよう求められる。Sapetら（2019）の設定に従い、テストセットからランダムに選択した100のイベントを評価する。各イベントと関係性のタイプについて、beamsearchを用いて10個の候補が生成され、5人の異なる作業者によってフルビームが評価される。全体として、1つの関係につき $n=5000$ の評価が生成される（100イベント×5ワーカー×10候補）。表2のAvgは、これらのスコアの平均値であり、各モデルの総評価数は $n=45000$ である。統計的有意性の検定には、100k個の順列を用いたPitmanの検定（Noreen, 1989）を用いる。50の異なる仮説が検証されるため（9つの関係＋合計）、有意性の閾値を補正するためにホルム-ボンフェローニ法（Holm, 1979）が使用される。開発セットからのイベント例とその生成されたフレーズオブジェクトは表5にある。

ベースライン：Sap et al.(2019) で学習された、LSTM sequence-to-sequenceモデル (Sutskever et al., 2014) を用いて入力のサブジェクトと関係を符号化して出力オブジェクトを生成するモデルに対する我々の手法の性能を報告する。

アブレーション：また、大規模なコーパスでの事前学習がモデルの知識生産学習にどのように役立つかを評価するため、事前学習済みの重みを初期化しないバージョンのCOMET（COMET(-pretrain)）を訓練する。最後に、本手法の最終目標は高品質で多様な知識ベース構築を可能にすることであるため、様々なデコーディング方法が候補となる知識タプルの品質にどのような影響を与えるかを調査する。具体的には、argmax greedy decoding、ビームサイズb=2, 5, 10のbeamsearch、k=5, 10のtop-ksam-plingの3つの復号化方式について、その効果を検証する。各復号化方法について、各方法で生成された最終候補の数について、人間による評価を行った。

4.2 結果

総合性能：表1のBLEU-2の結果から、COMETはすべてのベースラインの性能を上回り、Sapら（2019）のトップパフォーマンスモデルに対して51%の相対的な改善を達成したことがわかる。しかし、より興味深いのは、人間による評価の結果であり、COMETは、トップのベースラインであるEvent2IN(VOLUN)に対して18%の統計的に有意な相対Avgパフォーマンスの増加を報告した。この性能向上は、すべての関係タイプにおいて一貫しており、改善が確認されている。また、表1には、品質向上に加えて、COMETがベースラインよりも多くの新規タプルオブジェクトを生成していることが示されている。

言語からの知識の学習Radfordら（2018）のGPTモデルから事前に訓練したパラメータで重みを初期化したモデルの性能とランダム初期化から訓練した同じアーキテクチャのモデル間で有意差も観察された。この14%の相対的な改善により、GPTモデルで学習した言語表現が自然言語のコモンセンス知識の生成に転用可能であることが確認された。

デコードアルゴリズムの効果：表3では、異なる生成ポリシーが知識の質に与える影響を示している。最も興味深い結果は、知識エッジタプルを生成するために貪欲なデコードを使用すると、ATOMICテストセットの人間による評価と比較して、相対的に10%のパフォーマンスギャップしか生じないことであり、モデルが生成する知識は人間のパフォーマンスに近づいていることを示している。より多くの候補を作成すると全体的なパフォーマンスは低下するが、ビームサイズが10の場合、品質評価は55%程度で推移している。この結果は、生成されたタプルの正しさを確認するために人間の評価者がループ内にいることで、COMETが効果的であることを示唆している。

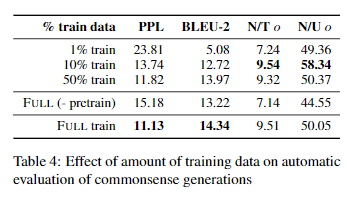
シードタプルからの学習の効率化：すべてのドメインに、訓練に利用できる大規模なコモンセンスKBがあるとは限らないため、学習に利用できる訓練データの量を変えることで、生成する知識の品質と新規性にどのように影響するかを調査した。表4の結果から、利用可能な訓練データが10%しかない場合でも、モデルは首尾一貫した、適切で、新規性のある世代を生成できることがわかった。1%の訓練データしか使用しない場合、生成される応答品質は著しく低下し、品質と新規性の両方の指標において、観測された結果は著しく低くなった。興味深いことに、事前に訓練した重みを用いないモデルの訓練は、シードタプルの10%を用いた訓練に匹敵する性能を示し、事前に訓練した言語表現を用いることの影響を定量的に示している。

5 ConceptNet実験

Liら(2016)が提供するConceptNetデータセットは、ConceptNet 5(Speer et al., 2017)のOpenMind Common Sense (OMCS) エントリから得られたタプルから構成されています。タプルはスタンダート $sro$ フォーム - (e.g., take a nap, Causes, have energy)になっている。最も信頼性の高い1200タプルはテストセットの作成に使用され、次の1200タプルは2つの開発セットの作成に使用され、我々はこの作業で組み合わせる。トレーニングセットの100kバージョンはモデルのトレーニングに使用され、34の関係タイプを含んでいる。

5.1 セットアップ

指標：ConceptNet関係を生成するモデルを以下の指標で評価する。まず、テストセット（PPL）に含まれるゴールド関係の複雑さを報告する。また、生成された知識の質を評価するために、Liら（2016）によって開発された事前学習済みのBilinear AVGモデルによって正しいと評価されたテストセット内の生成された正の例の数を報告する。与えられた $sro$ タプルに対して、このモデルは、タプルが正しいかどうかの確率を生成する。Lietら(2016)で提案された完了タスクにおいて、このモデルはテストセットで92.5%の精度を達成し、生成されたタプルが正しいかどうかを自動的に評価する強力な代理であることが示された。最後に、ATOMICと同じ新規性メトリクスである、N/TsroとN/Toを報告する。

ベースライン：ベースラインとして、Saitoら(2018) が提案したBiLSTMモデルを、付録A.2で概説したマイナーチェンジを加えて再実装する。このモデルは、知識ベース補完モデルを補強するのに役立つように、 $sr→o$ と $or→st$ の両方向で知識をエンコードすることを学習するように訓練されている。しかし、このモデルは $sr→o$ タプルの生成タスクでのみ評価されている。また、後の研究のために、 $sr→o$ タスクのみで学習させたLSTMモデル（LSTM -s）の結果も掲載する。

アブレーション：私たちのフルモデルには、以下のようなアブレーションが含まれている。まず、大規模コーパス（Radford et al., 2018）での事前学習がパフォーマンスにどのように役立つか、表6でCOMET(- pretrain)と表記した比較モデルをゼロから訓練することで評価する。第二に、我々のメインモデルでは、関係名を自然言語（例えば、IsA→"is a";　HasSubevent→"has subevent"）にマッピングし、各関係に対してゼロから特別な埋め込みを学習するのではなく、モデルが言語を使ってこれらの概念を表現することを学習できるようにしている（Levy et al., 2017）。また、関係トークンを自然言語に変換しないモデル（例：ISA $\nrightarrow$ "is a"）を学習し、これをCOMET-RELTOKと呼ぶことにする。

5.2 結果

品質：我々の結果は、質の高い知識を生成することができることを示すものである。表6にある低いperplexityスコアは、予測に対するモデルの高い信頼性を示し、高い分類スコア（95.25%）は、Li et al（2016）のKB補完モデルが生成されたタプルをほとんどのケースで正しいものとしてスコア付けしていることを示している。この高いスコアは、敵対的な生成が原因である可能性があるが、人間による評価（ATOMICと同じデザインに従う）では、簡単にデコードされたタプルの91.7%が正しいとして評価された。また、表7に示したランダムに選択された例も、モデルによって生成された知識の質の高さを示している。

新規性：高品質であることに加え、COMETによって生成されたタプルは新規性も持っており、タプルの59.25%は訓練セットには存在しない。これは、モデルがノード間の新しい辺を生成し、さらに新しいノード（ノードの3.75%が新規）を生成して知識グラフのサイズを拡張できることを示した。しかし、新規生成はトレーニングセットのタプルを単純化したものであることがある。例えば、表7では、"doctor CapableOf save life"というタプルはトレーニングセットには存在しないが、"doctor CapableOf save person life "は存在する。しかし、"bird bone HasProperty fragile "や "drift wood AtLocation beach "のように、トレーニングセットに関連タプルが存在しない、全く新しいタプルも多い。

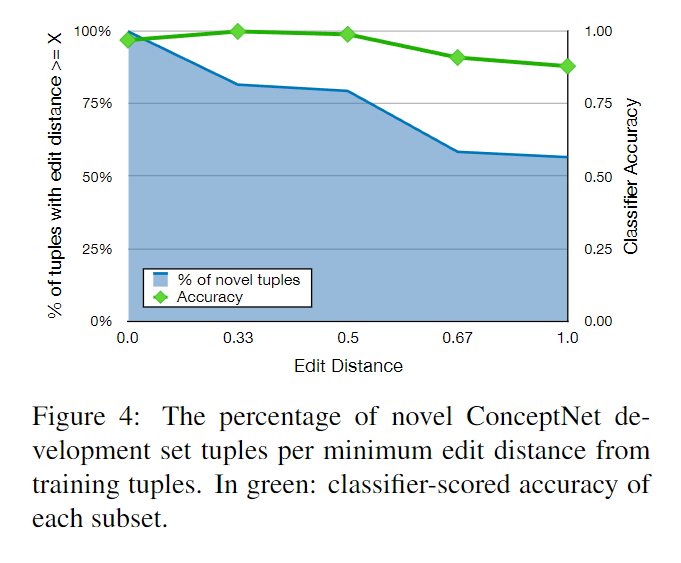
　さらに、開発セットの新規タプルは、トレーニングセットのフレーズオブジェクトと、同じ $s,r$ のフレーズオブジェクトの最小編集距離でどれだけ異なるかを調査する。フレーズオブジェクト $o_{dev}$ の編集距離は、タプル $(s, r, o_{dev} )$ から、最も近い訓練用タプル $(s, r, o_{trn} )$ の編集距離と比較して測定される。編集距離は単語トークン（ストップワードを除く）を用いて測定し、 $o_{dev}$ または $o_{trn}$ の最大単語数で正規化する。編集距離の最大値は1（つまり全く異なる単語列）、最小値は0（つまりストップワードを除いた同じ単語列）であり、編集距離の最大値は1（つまり全く異なる単語列）、最小値は0（つまりストップワードを除いた同じ単語列）である。図4は、最も近いトレーニングセットタプルとの編集距離が少なくともX軸の値である新規開発セットタプルのパーセンテージを示したものである。 75%以上の新規フレーズタプルは、訓練フレーズオブジェクトとの正規化編集距離が0.5以上であり、新規フレーズオブジェクトのほとんどが、訓練セット内の最も近い類似物と著しく異なる単語配列を持っていることを示している。

言語からの知識の学習：ATOMICと同様に、大規模な言語コーパスでCOMETを事前学習することが、常識の一般化能力にどのように影響するかを調べた。この効果は表6で明らかであり、事前訓練されたCOMETは、ランダムに初期化されたモデルよりも、自動評価と人間評価で明らかに向上している。トレーニングセットには存在しない "mangoIsAfruit "というタプルが生成され、表7でこの効果を確認することができる。トレーニングセットで "mango "エンティティを含む唯一のタプルは "mangoUsedForsalsa "で、これは十分に情報を提供ししない。確認として、COMET（-pretrain）の出力が "mangoIsAspice "であることを見ますが、これは知識の種集合にある "mango "に関する情報を考えると妥当な推論であると考えられる。

言語による関係表現：記号による関係表現と自然言語による関係表現のモデルを比較した場合、自動的な指標は重要な差異を示さないが（表6）、関係を言語として表現することの利点については、事例から定性的な洞察を得ることができる。 ConceptNetの学習セットでは、"dove"に対する非鳥類学的な参照は"dove CapableOf fly"のみであるが、我々のモデルは一般化を学習して"dove SymbolOf purity"というタプルを生成している。シンボル関係詞を用いたモデルでは、"dove SymbolOf submarine "という関係しか生成できず、これは "submarine "と "dove "のより海っぽい（そして関連性のない）語義を関連付けるようである。

6 関連研究

知識ベース構築：これまでの研究では、専門家の知識を利用した再論理スキーマとしての知識ベースの構築（Lenat,1995; Bodenreider, 2004; Miller, 1995）、半構造化テキスト抽出（Suchanek et al, 2007;Hoffart et al, 2013; Auer et al, 2007; Bollacker et al, 2008）および非構造化テキスト抽出（Dong et al, 2014; Carlson et al, 2010; Nakasholeet al, 2011, 2012; Niu, 2012）が研究された。我々の研究では、明確に定義された関係スキーマ構造ではなく、オープンテキストのイベントの使用を必要とする常識的な知識ベースの構築に焦点を当てる。情報抽出の他の研究は、オープンテキストエンティティを用いた知識ベース構築に適用することもできるが（Soderland et al., 2010; Etzioni et al., 2011; Fader et al., 2011; Mausam et al., 2012; Fan et al., 2010; Cui et al., 2018）、これらの方法は通常、明示的なテキスト再列を抽出する。逆に、我々のアプローチは、コモンセンス情報が一般的であるように、しばしばテキストに記載されていない新しい知識を生成する（Gordon and Van Durme, 2013）。

コモンセンス知識ベースの補完：新しいコモンセンス知識の生成に関する既存の研究は、ConceptNetとATOMICを基礎KBとして使用している。具体的には、Liら(2016)は、ConceptNetのタプルをスコアリングするための一連のニューラルネットワークモデルを提案した。我々の研究は、彼らのモデルが知識グラフの新しいノードを作るためのフレーズを生成するために学習するのではなく、完全なタプルを評価するので、このアプローチとは異なるものである。Saitoetら2018)は、コモンセンスタプルの補完と生成のための共同モデルを提案することによって、この仕事を構築している。しかし、彼らの研究は、非合理的なKB構築のカバレッジを高めるためではなく、KBの補完モデルを補強するためにタプル生成を使用することに焦点を当てている。最後に、Sapら(2019)は、LSTMエンコーダ-デコーダモデルを使用して、社会的状況についてのコモンセンス知識を生成する。我々は、トランスフォーマーを使用し、それらを初期化するために事前に訓練された言語表現（Radford et al., 2018）を使用することの効果を調査する。

トランスフォーマーと事前学習：最後に、我々の仕事は、様々なシーケンスラベリング、分類、およびNLIエンドタスクのための事前訓練された言語モデルの適応に関する以前の仕事（Radford et al., 2018; Peters et al., 2018; Devlin et al., 2018）に基づいている。私たちの研究は、新しいグラフノードとノード間のエッジを生成することにより、事前に訓練された言語モデルを大規模なコモンセンスKB構築にどのように使用できるかを調査している。

7 結論

常識的な知識ベースを自動構築するためのCOMmonsenseTransformers(COMET)を紹介する。COMETは、言語モデルの重みを適応させ、新規かつ多様な常識知識タプルを生成するように学習する枠組みである。ATOMICとConceptNetの2つの常識知識ベースに関する実証結果は、人間の評価者が正しいとみなす新規の常識知識をCOMETが頻繁に生成することを示している。これらのポジティブな結果は、他の様々なタイプの知識ベースにアプローチを拡張すること、また、COMETが任意の知識シードに対してOpenIEスタイルの知識タプルを生成することを学習できるかどうかを調査することを今後の課題としている。

2023-06-12

今日の論文2023/06/11,12：LUKE: Deep Contextualized Entity Representations with Entity-aware Self-attention

今日の論文

LUKE: Deep Contextualized Entity Representations with Entity-aware Self-attention

aclanthology.org

Ikuya Yamada, Akari Asai, Hiroyuki Shindo, Hideaki Takeda, and Yuji Matsumoto. 2020. LUKE: Deep Contextualized Entity Representations with Entity-aware Self-attention. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), pages 6442–6454, Online. Association for Computational Linguistics.

License: Creative Commons Attribution 4.0 International License(CC-BY)

本記事は、原著の内容に基づき筆者が要約または翻訳したものです。以下の図は、そこから引用しています。

This article is my summary or translation based on the content of the original publication. The following figures are taken from it.

要点まとめ

エンティティ表現は、エンティティを含む自然言語タスクにおいて有用である。本論文では、双方向トランスフォーマー（Vaswani et al., 2017）に基づく、単語とエンティティの新しい事前学習された文脈化された表現を提案する。提案モデルは、与えられたテキスト内の単語とエンティティを独立したトークンとして扱い、それらの文脈化された表現を出力する。我々のモデルは、BERTのmasked language model (Devlin et al, 2019)に基づく新たな事前学習課題を用いて学習される。このタスクは、Wikipediaから取得した大規模なエンティティ注釈付きコーパスにおいて、ランダムにマスクされた単語とエンティティを予測することを含む。また、我々は、トランスフォーマーのセルフアテンションメカニズムを拡張した、エンティティを考慮したセルフアテンションメカニズムを提案し、アテンションスコアを計算する際にトークン（単語またはエンティティ）の種類を考慮する。提案モデルは、様々なエンティティ関連タスクにおいて、経験的に優れた性能を達成した。特に、5つの有名なデータセットにおいて、SoTAの結果を得ることができた： Open Entity（エンティティタイピング）、TACRED（関係分類）、CoNLL-2003（名前付きエンティティ認識）、ReCoRD（クローズ型質問応答）、SQuAD 1.1（抽出型質問応答）。ソースコードと学習済み表現は、https://github.com/studio-ousia/luke で公開した。

github.com

1 序論

自然言語のタスクには、関係分類、エンティティタイピング、名前付きエンティティ認識（NER）、質問応答（QA）など、エンティティを含むものが多い。このようなエンティティ関連のタスクを解決する鍵は、エンティティの効果的な表現を学習するモデルである。従来のエンティティ表現は、知識ベース（KB）内のエンティティに関する情報を格納する固定埋め込みベクトルを各エンティティに割り当てる（Bordes et al., 2013; Trouillon et al., 2016; Yamada et al., 2016, 2017）。これらのモデルはKBの豊富な情報を捉えているが、テキスト中のエンティティを表現するためにエンティティリンクが必要であり、KBに存在しないエンティティを表現することができない。

これに対して、BERT (Devlin et al., 2019) やRoBERTa (Liu et al., 2020) などのTransformer (Vaswaniet al., 2017) に基づく文脈化単語表現 (CWR) は、言語モデリングに基づく教師なし事前学習タスクで学習した効率的な汎用単語表現を提供する。最近の多くの研究では、CWRに基づいて計算されたエンティティの文脈化表現を使用して、エンティティ関連のタスクを解決している（Zhang et al., 2019; Peters et al., 2019; Joshi et al.,2020）。しかし、CWRのアーキテクチャは、以下の2つの理由から、エンティティを表現するのに適していない。 (1) CWRはエンティティのスパンレベルの表現を出力しないため、通常、下流のデータセットに基づき、そのような表現を計算する方法を学ぶ必要がある。 (2) 多くのエンティティ関連タスク、例えば、関係分類やQAは、エンティティ間の関係を推論する。トランスフォーマーは、セルフアテンション機構を用いて単語を複数回関連付けることで単語間の複雑な関係性を捉えることができるが（Clark et al., 2019; Reif et al., 2019）、多くのエンティティがモデル内で複数のトークンに分割されているため、エンティティ間でそのような推論を行うことは困難である。さらに、CWRの単語ベースの事前学習タスクは、エンティティの他の単語を与えられたマスクドワードを予測すること、例えば、"The Lord of the [MASK]" を与えられた "Rings" を予測することは、エンティティ全体を予測するよりも明らかに簡単だからである。

　本論文では、LUKE（Language Understanding with Knowledge-based Embeddings）を開発することによって単語とエンティティに関する新しい事前学習済みの文脈化表現を提案している。LUKEは、Wikipediaから取得した大量のエンティティ注釈付きコーパスを用いて訓練したTransformer（Vaswani et al., 2017）に基づいている。LUKEと既存のCWRの重要な違いは、単語だけでなくエンティティも独立したトークンとして扱い、Transformerを用いてすべてのトークンの中間表現と出力表現を計算することである（図1参照）。LUKEは、BERTのmasked language model (MLM)（Devlin et al., 2019）をストレートに拡張した新しい事前学習タスクを使って学習される。

　LUKEは、BERTのmasked language model (MLM)（Devlin et al., 2019）をそのまま拡張した新しい事前訓練タスクを用いて訓練されます。このタスクは、[MASK]エンティティに置き換えることでランダムにエンティティをマスクし、これらのマスクされたエンティティのオリジナルを予測することによってモデルを訓練する。RoBERTaをベースとし、MLMと提案タスクの目的を同時に最適化することで、モデルの事前学習を実施する。下流のタスクに適用した場合、[MASK]エンティティを入力として、テキスト中の任意のエンティティの表現を計算することが可能である。さらに、タスクにエンティティ注釈がある場合、このモデルは、対応するエンティティ埋め込みにエンコードされた豊富なエンティティ中心情報に基づいて、エンティティの表現を計算することができる。

　本論文のもう一つの重要な貢献は、エンティティを意識したセルフアテンション機構を用いてTransformerを拡張した点である。既存のCWRとは異なり、我々のモデルは単語とエンティティという2種類のトークンを扱う必要がある。そのため、トークンの種類を容易に判別できるようにすることが有益であると考えるそのため、アテンディングトークンとアテンディングされたトークンに応じて異なるクエリ機構を採用することで、自己アテンション機構を強化した。

　　我々は、エンティティタイピング、関係分類、NER、クローズ型QA、および抽出QAという5つの標準エンティティ関連タスクに対して大規模な実験を実施し、我々の提案モデルの有効性を検証している。提案モデルは、RoBERTaを含む全てのベースラインモデルを全ての実験で上回り、5つのタスクでSoTAの結果を得た：Open Entityデータセットでのエンティティタイピング(Choi et al., 2018)、TACREDデータセットでの関係分類（Zhang et al., 2017）、CoNLL-2003データセット（Tjong Kim Sang and De Meulder, 2003）のNER、ReCoRDデータセットのクローズ型QA（Zhang et al., 2018a）、SQuAD 1.1 dataset（Rajpurkar et al., 2016）の抽出的QA。ソースコードと事前学習した表現を https://github.com/studio-ousia/luke で公開している。本論文の主な貢献は以下のように要約される：

我々は、エンティティに関連するタスクに対応するために特別に設計された新しいコンテキスト付きリプレゼンテーションであるLUKEを提案する。LUKEは、Wikipediaから得られた大量のエンティティ注釈付きコーパスを用いて、ランダムにマスクされた単語や実体を予測するように訓練される。
本論文では、Transformerの原型を効果的に拡張した、エンティティを意識したセルフアテンション機構を紹介する。提案する機構は、アテンションスコアを計算する際に、トークンのタイプ（単語や属性）を考慮する。
LUKEは、5つの一般的なデータセットにおいて、強力な経験的性能を達成し、SoTAの結果を得ることができた： Open Entity、TACRED、CoNLL-2003、ReCoRD、SQuAD 1.1です。

2 関連研究

静的なエンティティ表現：従来のエンティティ表現は、KB内の各エンティティに固定的な埋め込みを割り当てている。これには、知識グラフで学習した知識埋め込み（Bordes et al., 2013; Yang et al., 2015; Trouillon et al.,2016）や、KBから取得したエンティティのテキストコンテキストや説明で学習した埋め込み（Yamada et al., 2016, 2017; Cao et al., 2017; Ganeaand Hofmann, 2017）がある。我々の事前学習タスクと同様に、NTEE（Yamada et al., 2017）とRELIC（Ling et al., 2020）は、KBから取得したそのテキストコンテキストを与えられたエンティティを予測することによってエンティティ埋め込みをトレーニングするアプローチを使用している。テキスト中のエンティティを表現する場合、このラインの主な欠点は、（1）エンティティを表現するためにテキスト中のエンティティを対応するKBエントリに解決する必要があり、（2）KBに存在しないエンティティを表現できないことである。

文脈化単語表現：最近の多くの研究では、CWRの単語表現を使用して計算されたテキスト中のエンティティの文脈に応じて表現に基づいてエンティティ関連タスクに取り組んでいる（Zhang et al, 2019; Baldini Soares et al., 2019; Peters et al., 2019; Joshi et al., 2020; Wang et al., 2019b, 2020）。CWRの代表的な例は、ELMo（Peters et al., 2018）とBERT（Devlin et al., 2019）で、それぞれ深いlong short-temr memory（LSTM）とTransformer（Vaswani et al., 2017）に基づいている。BERTは、テキスト内のランダムな単語をマスクし、マスクされた単語を予測するためにモデルを訓練する事前学習タスクであるMLMを使用して訓練される。 RoBERTa（Liu et al, 2020）、XLNet（Yang et al., 2019）、Span-BERT（Joshi et al., 2020）、ALBERT（Lan et al., 2020）、BART（Lewis et al., 2020）、T5（Raffelet et al., 2020）などの最近のCWRのほとんどは、MLMと同等または類似のタスクを用いて訓練したTransformerをベースにしている。単語ではなくエンティティをマスクする我々の提案する事前学習タスクと同様に、最近のいくつかのCWR、例えばSpan-BERT、ALBERT、BART、T5は、単一の単語ではなく単語スパンをランダムにマスクすることによってMLMを拡張している。

　さらに、最近の様々な研究では、KBのような外部ソースからの知識を注入することによってCWRを強化する方法が模索されている。ERNIE（Zhang et al., 2019）やKnow-BERT（Peters et al., 2019）は、KBから別途学習した静的エンティティ埋め込みを使用してCWRを強化するために同様のアイデアを使用している。WKLM（Xiong et al., 2020）は、テキスト内のエンティティ名が同じタイプの別のエンティティ名で置換されているかを検出するモデルを訓練する。KEPLER（Wang et al, 2019b）は、MLMと知識埋め込み目的関数（Bordes et al., 2013）に基づいて事前学習を行う。 K-Adapter（Wang et al., 2020）は、我々の研究と同時に提案されたもので、事実と言語の知識を注入するニューラルアダプターを使用してCWRを拡張するものである。この研究は、私たちの事前学習タスクがKBの情報を使ってモデルを強化することから、私たちの研究と関連している。

　LUKEは、上記のCWRとは異なり、エンティティに関連するタスクを効果的に解決するために設計された、エンティティを意識したセルフアテンション機構を備えた改良型トランスフォーマーアーキテクチャを使用している。 LUKEは、すべての実験において、既存のCWRや知識強化型CWRに対して優れた実証結果を得ている。すべての実験において、既存のCWRや知識強化型CWRより優れた実証結果を得ることができた。

3 LUKE

図 1 に LUKE のアーキテクチャを示す。モデルは多層双方向トランスフォーマーを採用している（Vaswani et al., 2017）。文書中の単語とエンティティを入力トークンとして扱い、各トークンの表現を計算する。例えば、 $m$ 個の単語 $w_1, w_2, \ldots ,w_m$ と $n$ 個のエンティティ $e_1, e_2, \ldots, e_n$ からなるシーケンスが与えられたとき、我々のモデルは、 $D$ 次元の単語表現 $h_{w_1}, h_{w_2}, \ldots ,h_{w_m}$ 、ここで、 $h_w \in \mathbb{R}^D$ とエンティティ表現 $h_{e_1}, h_{e_2}, \ldots, h_{e_n}$ 、ここで $h_e \in \mathbb{R}^D$ を計算する。エンティティは、Wikipediaのエンティティ（例：図1のBeyonc）またはスペシャルエンティティ（例：[MASK]）とすることができる。

3.1 入力表現

トークン（単語またはエンティティ）の入力表現は、以下の3つの埋め込みを使用して計算される。

トークン埋め込みは、対応するトークンを表す。単語トークン埋め込みを $A \in \mathbb{R}^{V_w×D}$ とし、ここで $V_w$ は語彙の数である。計算効率を上げるため、エンティティトークン埋め込みを2つの小さな行列、 $B \in \mathbb{R}^{V_e×H}$ と $U \in \mathbb{R}^{H×D}$ に分解して表現する（ここで、 $V_e$ は語彙の中のエンティティ数）。したがって、エンティティトークン埋め込みの完全な行列は $BU$ と計算できる。
位置埋め込みは、単語列におけるトークンの位置を表す。単語列の $i$ 番目の位置に出現する単語とエンティティは、それぞれ $C_i \in \mathbb{R}^D$ と $D_i \in \mathbb{R}^D$ として表現される。エンティティ名が複数の単語を含む場合、図1に示すように、対応する位置の埋め込みを平均化することでその位置の埋め込みが計算される
エンティティタイプの埋め込みは、トークンがエンティティであることを表す。埋め込みは、 $e \in \mathbb{R}^D$ で示される単一のベクトルである。

単語の入力表現とエンティティの入力表現は、それぞれトークンと位置の埋め込み、およびトークンと位置とエンティティタイプの埋め込みを合計することで計算される。過去の研究（Devlin et al., 2019; Liu et al., 2020）に従い、特別なトークン[CLS]と[SEP]を、それぞれ最初と最後の単語として単語列に挿入する。

3.2 エンティティを意識したセルフアテンション

セルフアテンション機構は、トランスフォーマー（Vaswani et al, 2017）の基礎であり、トークンの各ペア間のアテンションスコアに基づいて、トークン同士を関連付ける。 $x_i \in \mathbb{R}^D$ の入力ベクトル $x_1, x_2, \ldots, x_k$ の列が与えられたとき、 $y_i \in \mathbb{R}_L$ の出力ベクトル $y_1, y_2, \ldots, y_k$ の各々は、変換された入力ベクトルの加重和に基づいて計算される。ここで、各入出力ベクトルは、本モデルにおけるトークン（単語またはエンティティ）に対応するため、 $k=m+n$ とする。 $i$ 番目の出力ベクトル $y_i$ は次のように計算される：

ここで、 $Q \in \mathbb{R}^{L×D}$ , $K \in \mathbb{R}_{L×D}$ , $V \in \mathbb{R}^{L×D}$ はそれぞれ、クエリ行列、キー行列、バリュー行列を表す。

　LUKEは単語とエンティティの2種類のトークンを扱うため、アテンションスコア（ $e_{ij}$ ）を計算する際に、対象となるトークンの種類の情報を用いることが有益であると考えられる。そこで、 $x_i$ と $x_j$ のトークンの種類ごとに異なる問い合わせ行列を使用する、エンティティを意識したクエリ機構を導入し、この機構を強化する。形式的には、アテンションスコア $e_{ij}$ は以下のように計算される：

ここで、 $Q_{w2e}, tex: Q_{e2w}, Q_{e2e} \in \mathbb{R}^{L×D}$ はクエリ行列である。オリジナルの機構と我々の提案する機構の計算コストは、学習時に勾配の計算と追加クエリ行列のパラメータの更新を行う追加コストを除いて同一であることに注意されたい。

3.3 事前学習タスク

LUKEの事前学習には、従来のMLMと、MLMを拡張してエンティティ表現を学習する新しい事前学習タスクを使用する。特に、Wikipediaのハイパーリンクをエンティティの注釈として扱い、Wikipediaから取得した大規模なエンティティの注釈付きコーパスを用いてモデルを学習する。ある割合のエンティティをランダムにマスクし、特別な[MASK]エンティティに置き換えて、マスクされたエンティティを予測するモデルを学習する。形式的には、語彙のすべてのエンティティに対してソフトマックス関数を適用することで、マスクされたエンティティに対応する元のエンティティが予測される：

ここで、 $h_e$ はマスクされたエンティティに対応する表現、 $T \in \mathbb{R}^{H×D}$ 及び $W_h \in \mathbb{R}^{D×D}$ は重み行列、 $b_o \in \mathbb{R}^{V_e}と[tex: b_h \in \mathbb{R}^D$ はバイアスベクトル、 $gelu（\cdot）$ はgelu活性化関数（Hendrycks and Gimpel, 2016）、 $\text{layer_norm} (\cdot)$ はレイヤーノーム関数（Lei Ba et al., 2016）である。最終的な損失関数は、MLM損失とマスクされたエンティティを予測するためのクロスエントロピーの損失の合計であり、後者は前者と同じように計算される。

3.4 モデリングの詳細

我々のモデル構成は、 $\text{RoBERTa_{LARGE}}$ （Liu et al., 2020）、双方向トランスフォーマーとBERT（Devlin et al., 2019）の変種に基づく事前訓練済みCWRに従う。特に、我々のモデルは、 $D= 1024$ の隠れ次元、24の隠れ層、 $L= 64$ のアテンションヘッド次元、16のセルフアテンションヘッドを持つ双方向トランスフォーマーに基づいている.エンティティトーク埋め込みの次元数は $H= 256$ に設定されている。RoBERTaのパラメータは355M、エンティティのパラメータは128Mであり、パラメータ総数は約483Mである。入力テキストはRoBERTaのトークナイザーを用いて単語にトークン化され、 $V_w=50K$ 単語の語彙で構成される。計算効率のため、エンティティ語彙はすべてのエンティティを含まず、エンティティ注釈に最も頻繁に登場する $V_e= 500K$ エンティティのみを含む。また、エンティティ語彙には、[MASK]と[UNK]という2つの特殊エンティティが含まれている。

　このモデルは、Wikipediaのページをランダムな順序で200Kステップ繰り返し学習させる。学習時間を短縮するために、LUKEがRoBERTaと共通に持つパラメータ（トランスフォーマーと単語の埋め込みのパラメータ）をRoBERTaで初期化する。過去の研究（Devlin et al., 2019; Liu et al., 2020）に従い、全単語とエンティティの15%をランダムにマスクする。我々は、自己アテンション機構のアブレーション研究を行いたいが、2回の事前学習を行う余裕がないため、我々のエンティティを意識したセルフアテンション機構ではなく、オリジナルのセルフアテンション機構を使用して事前学習を行う。セルフアテンション機構のクエリ行列（ $Q_{w2e}$ 、 $Q_{e2w}$ 、そして $Q_{e2e}$ ）は、下流のデータセットを用いて学習する。事前学習の詳細については、付録Aに記載されている。

4 実験

我々は、エンティティタイピング、関係分類、NER、クローズ型QA、抽出型QAという5つのエンティティ関連タスクを用いた大規模な実験を実施した。我々は、単語、エンティティ、またはその両方の表現に単純な線形分類器を乗せた類似のモデル構造をすべてのタスクに使用する。特に指定がない限り、[CLS]と[SEP]のトークンをそれぞれ最初と最後のトークンとして元の単語列に挿入することによって、入力単語列を作成する。入力エンティティ列は、[MASK]エンティティ、タスクのために導入された特別なエンティティ、またはWikipediaエンティティを使用して構築される。タスク固有の特殊エンティティのトークン埋め込みは[MASK]エンティティのそれを使って初期化され、エンティティを意識したセルフアテンション機構のクエリー行列（ $Q_{w2e}$ 、 $Q_{e2w}$ 、 $Q_{e2e}$ ）は元のクエリー行列 $Q$ を使って初期化される。

事前学習ではRoBERTaをベースモデルとして使用したため、すべてのタスクでRoBERTaを主要なベースモデルとして使用する。各セクションのベースライン・モデルについては、セクション 2 で説明しているため、説明を省略する。実験の詳細については、付録Bを参照されたい。

4.1 エンティティタイピング

まず、与えられた文中のエンティティの種類を予測するタスクであるエンティティタイピングの実験を行う。 Zhangら（2019）に従い、Open Entityデータセット（Choi et al., 2018）を使用し、9つの一般的なエンティティタイプのみを考慮する。Wangら（2020）に従い、loose micro-precision、recall、F1を報告し、主要指標としてmicro-F1が採用されている。

モデル：対象エンティティを[MASK]エンティティで表現し、各文中の単語とエンティティをモデルに入力する。そして、対応するエンティティ表現に基づき、線形分類器を用いてエンティティを分類する。このタスクをマルチラベル分類として扱い、すべてのエンティティタイプで平均化された2値のクロスエントロピー損失を用いてモデルを訓練する。

ベースライン：UEFT（Choi et al., 2018）は、双方向LSTMを利用してコンテキスト表現を計算する便利なモデルである。また、BERT、RoBERTa、ERNIE、KnowBERT、KEPLER、K-Adapterをベースラインとして使用する。

結果：表1に実験結果を示す。LUKEは、主要ベースラインのRoBERTaを2.0 F1ポイント、先行する最良公開モデルのKnowBERTを2.1 F1ポイント大幅に上回る。さらに、LUKEはK-Adapterを0.7 F1ポイント上回り、新たなSoTAを獲得しています。

4.2 関係性分類

関係分類は、文中のheadエンティティとtailエンティティ間の正しい関係を決定する。我々は、42種類の関係を持つ106,264文を含む大規模な関係分類データセットであるTACRED dataset（Zhang et al., 2017）を用いて実験を実施する。 Wangら（2020）に従い、micro-precision、recall、F1を報告し、micro-F1を主要指標とする。

モデル：頭部と尾部の実体を表すために、それぞれ[HEAD]と[TAIL]という二つの特殊エンティティを導入し、各文中の単語とこの二つのエンティティをモデルに入力する。次に、headとtailのエンティティを結合した表現に基づく線形分類器を使用してタスクを解く。このモデルは、クロスエントロピー損失を用いて学習される。

ベースライン：C-GCN（Zhang et al., 2018b）は、依存関係木構造上のグラフ畳み込みネットワークを用いてタスクを解決する。MTB（Baldini Soareset al., 2019）は、大量のエンティティ注釈付きテキストを用いた空白マッチングタスクを通じてBERTに基づいて関係表現を学習する。また、LUKEをBERT、RoBERTa、SpanBERT、ERNIE、KnowBERT、KEPLER、K-Adapterと比較した。

結果：実験結果は表2に示す。 LUKEは、我々の主要なベースラインであるRoBERTaを1.4 F1ポイント、以前の最良公開モデルであるMTBとKnowBERTを1.2 F1ポイント明らかに上回った。さらに、K-Adapterを0.7 F1ポイント上回り、新たなSoTAを達成した。

4.3 名前付きエンティティ認識

標準的なCoNLL-2003データセット（Tjong Kim Sang and De Meulder, 2003）を用いて、NERタスクの実験を行った。過去に行われた実験にならって、スパンレベルのF1を報告する。

モデル：Sohrab and Miwa（2018）に従い、各文中の可能なスパン（またはn-gram）をエンティティ名として列挙し、それらを対象エンティティタイプまたはスパンがエンティティではないことを示すノンエンティティタイプに分類することでタスクを解決する。データセットの各文に対して、可能な限りのスパンに対応する単語と[MASK]エンティティを入力する。各スパンの表現は、スパンの最初と最後の単語の単語表現と、スパンに対応するエンティティ表現を連結することによって計算される。その表現を使って線形分類器を用いて各スパンを分類し、交差エントロピー損失を用いてモデルを訓練する。計算効率を上げるため、16語以上のスパンは除外する。推論では、まず、ノンエンティティタイプに分類されたスパンをすべて除外する。重複するスパンを選択しないようにするため、予測されるエンティティタイプのロジットに基づいて残りのスパンから貪欲にスパンを選択し、すでに選択されているスパンと重複しない場合は降順に選択する。Devlinら（2019）に従い、ターゲット文書に最大限の文書コンテキストを含める。

ベースライン： LSTM-CRF（Lample et al., 2016）は、conditional random fields（CRF）付き双方向LSTMに基づくモデルである。Akbikら（2018）は、文字レベルの文脈化表現で強化したCRF付き双方向LSTMを用いてこの課題に取り組む。同様に、Baevskiら（2019）は、双方向トランスフォーマーに基づくCWRで強化されたCRF付き双方向LSTMを使用している。また、ELMo、BERT、RoBERTaをベースラインとして使用している。RoBERTaとの公正な比較を行うために、スパンの最初と最後の単語の表現を連結することによって計算されたスパン表現で、上記に記されたモデルを使用してその性能を報告する。

結果：実験結果を表 3 に示す。LUKEはRoBERTaを1.9 F1ポイント上回った。さらに、Baevskiet al.（2019）で報告された以前の状態を0.8 F1ポイント上回ることで、この競合データセットにおける新しいSoTAを達成した。

4.4 クローズ型質問応答

我々は、120K以上の例からなるクローズ型QAデータセットであるReCoRDデータセット（Zhang et al., 2018a）で我々のモデルを評価する。このデータセットの興味深い特徴は、その質問のほとんどが外部知識なしでは解決できないことである。以下は、このデータセットに含まれる質問とその回答の例である。

質問：訴訟の主張によると、「世界中の音楽ファンが瞬時に認識できる『天国への階段』の一部は、『X』の大部分とほぼ同じに聞こえる。」

答え：牡牛座

質問と文章が与えられたら、文章に書かれているエンティティのうち、欠けているエンティティ（上記の質問ではXで示されている）に適合するものを見つけることが課題である。このデータセットでは、文章中のエンティティスパン（開始位置と終了位置）のアノテーションが提供され、回答は提供されたエンティティスパンの中に1回または複数回含まれることになる。過去の研究成果に従い、開発セットとテストセットにおいて、完全一致（EM）とトークンレベルのF1を用いてモデルを評価した。

モデル：このタスクは、パスセージの各エンティティに関連性スコアを割り当て、最も高いスコアを持つエンティティを回答として選択することで解決される。Liuら（2020）に従い、質問 $q_1, q_2, \ldots, q_j$ と回答 $p_1, p_2, \ldots, p_l$ が与えられたとき、入力単語列は次のように構成される： $\text{ [CLS$ } q_1, q_2, \ldots,q_j \text{ [SEP ] [SEP ]} p_1, p_2, \ldots, p_l \text{ [SEP ]} ]。さらに、欠落したエンティティに対応する[MASK]エンティティと、パッセージ内のすべてのエンティティを入力する。欠損したエンティティと対応するエンティティを連結した線形分類器を用いて、パッセージ内の各エンティティの関連性スコアを計算する。パッセージ内の全エンティティを平均したバイナリクロスエントロピーロスを用いてモデルを学習し、最も高いスコア（ロジット）を持つエンティティを答えとして選択する。

ベースライン： DocQA+ELMo（Clark and Gardner, 2018）は、ELMo、bidirectional attention flow (Seo et al., 2017)、そしてセルフアテンション機構に基づくモデルである。XLNet+Verifier（Li et al., 2019）はXLNetに基づくルールベースの回答検証のモデルで、このデータセットに基づいて最近行われた競技会の優勝者である（Ostermann et al, 2019）。また、BERTとRoBERTaをベースラインとして使用する。

結果：その結果を表4に示す。LUKEは、開発セットにおいて、最良のベースラインであるRoBERTaをEMポイント1.8、F1ポイント1.9で大幅に上回った。さらに、モデルをアンサンブルしないテストセットでは、RoBERTa（アンサンブル）よりも優れた結果を得ることができた。

4.5 抽出的質問応答

最後に、100Kの質問と答えのペアからなる有名なStanford Question Answering Dataset（SQuAD）1.1 （Rajpurkar et al, 2016）を使って実験を行う。質問と答えを含むWikipediaの文章が与えられた場合、タスクはその文章に含まれる答えを予測することである。過去の研究に従って、開発セットとテストセットにおけるEMとトークンレベルのF1を報告する。

モデル：前の実験と同じ方法で、質問とパッセージから単語列を構築する。他の実験と異なり、Wikipediaのエンティティは、エンティティの名前（例："U.S."）から参照するエンティティ（例：United States）へのマッピングを使用して、質問と文章から自動的に生成されたエンティティ注釈に基づいてモデルに入力される。このマッピングは、付録Cで詳しく説明されているように、Wikipediaのエンティティハイパーリンクを使用して自動的に作成される。我々は、BERTとRoBERTaと同じモデルアーキテクチャを使用してこのタスクを解決した。特に、回答のスパン境界（すなわち、開始位置と終了位置）を予測するために、単語表現の上に独立した2つの線形分類器を使用し、交差エントロピー損失を使用してモデルを訓練する。

ベースライン：我々は、BERT、RoBERTa、SpanBERT、XLNet、ALBERTなどの最近のCWRの結果と我々のモデルを比較しました。RoBERTaとALBERTの結果は開発セットでのみ報告されているため、このセットを使用してこれらのモデルとの比較を行う。 RoBERTaとの公平な比較を行うため、RoBERTa（Liu et al., 2020）と同じモデル・アーキテクチャとハイパーパラメータを使用した。

結果：実験結果を表5に示す。LUKEは、開発セットにおいて、我々の主要なベースラインであるRoBERTaを0.9 EMポイント、0.4 F1ポイント上回った。さらに、この競争力のあるデータセットにおいて、EMとF1の両方でXLNetを0.3ポイント上回り、新たなSoTAを達成した。なお、XLNetはここで検討した他のモデルよりも、ビームサーチを含むより高度なモデルを使用している。

5 分析

このセクションでは、3つの追加実験を報告することで、LUKEの詳細な分析を提供する。

5.1 エンティティ表現による効果

LUKEの表現が下流タスクのパフォーマンスにどのような影響を与えるかを調べるために、CoNLL-2003データセットのNERとSQuADデータセットの抽出的QAを、エンティティを入力せずに行うアブレーション実験を行った。この設定では、LUKEは各単語の表現を計算するために単語配列のみを使用する。また、RoBERTaと同じモデル構成でタスクを処理した。表6に示すように、この設定では、CoNLL-2003データセットで1.4 F1ポイント、SQuADデータセットで0.6 EMポイントと、明らかに性能が低下し、この2つのタスクにおける我々のエンティティ表現の有効性を実証している。

5.2 エンティティを意識したセルフアテンションによる効果

LUKEを使用した場合の性能と、トランスフォーマー独自の機構を使用した場合の性能を比較することで、我々のエンティティを意識したセルフアテンション機構のアブレーションスタディを実施した。表7に示すように、LUKEは全てのタスクにおいて、エンティティを意識したセルフアテンション機構が元の機構を上回る性能を発揮している。さらに、関係分類（TACRED）とQA（ReCoRDとSQuAD）という2種類のタスクで大きな改善が見られた。これらのタスクは、エンティティ間の関係に基づく推論を含むため、本機構は、モデル（すなわち、アテンションヘッド）がエンティティ間の関係を捕捉することに容易に集中できるようにするものであると考えられる。

5.3 追加の事前学習の効果

セクション3.4で述べたように、LUKEはRoBERTaをベースに、Wikipedia コーパスを用いた200Kステップの事前学習を行っている。過去の研究（Liuet al., 2020; Lan et al., 2020）では、CWRの学習ステップ数を増やすだけで、下流タスクの性能が向上することが示唆されているため、RoBERTaと比較してLUKEの優れた実験結果は、事前学習ステップ数が多いために得られると考えられる。これを調べるために、RoBERTaに基づいて、Wikipedia コーパスを用いてMLMに基づく事前学習を追加したモデルを200K学習ステップ学習することにする。事前学習で使用した詳細な構成は、付録Aで確認できる。

　このモデルの性能をCoNLL-2003データセットとSQuADデータセットで評価したところ、RoBERTadと同じモデルアーキテクチャを使用していることがわかった。表8に示すように、このモデルは両データセットにおいてオリジナルのRoBERTaと同等の性能を達成しており、LUKEの優れた性能はより長い事前学習によるものではないことが分かる。

6 結論

本論文では、Transformerに基づく新しい事前学習された単語とエンティティの文脈化表現であるLUKEを提案する。LUKEは、改良されたTransformerアーキテクチャと、新しいエンティティを意識したセルフアテンションメカニズムを用いて、単語とエンティティのコンテキスト化された表現を出力する。実験結果は、様々なエンティティ関連のタスクにおいて、その有効性を証明している。今後の課題として、LUKEを生物医学や法律などのドメインに特化したタスクに適用する予定である。